

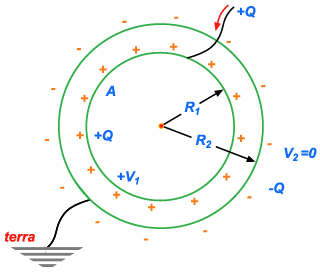
É
constituído por duas esferas concêntricas, de raios 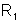 e
e 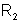 , separadas por um dielétrico de constante dielétrica
, separadas por um dielétrico de constante dielétrica
 . A esfera interna funciona como indutor. Para carregar
o condensador ligamos a armadura externa à terra e carregamos a
interna com a carga
. A esfera interna funciona como indutor. Para carregar
o condensador ligamos a armadura externa à terra e carregamos a
interna com a carga 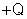 . A externa ficará com carga
. A externa ficará com carga 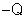 .
.
Para
calcular a capacidade precisamos calcular antes a diferença de potencial
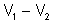 , e depois efetuar o quociente de Q por essa diferença.
, e depois efetuar o quociente de Q por essa diferença.
O
potencial  da esfera interna é a soma de dois potenciais: um
da esfera interna é a soma de dois potenciais: um
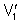 , produzido pela carga
, produzido pela carga 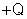 da própria esfera interna e outro,
da própria esfera interna e outro, 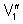 , produzido pela carga
, produzido pela carga 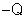 da esfera externa. O potencial que a carga
da esfera externa. O potencial que a carga 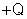 produz na esfera interna é:
produz na esfera interna é:
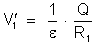
O
potencial que a carga 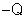 produz na superfície da armadura externa é
produz na superfície da armadura externa é 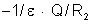 . Mas, vimos no tópico "Observações"
do capítulo 3 que o potencial no interior de um condutor
é igual ao potencial da sua superfície. Então a carga
. Mas, vimos no tópico "Observações"
do capítulo 3 que o potencial no interior de um condutor
é igual ao potencial da sua superfície. Então a carga 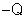 da armadura externa produz, na armadura interna, o potencial:
da armadura externa produz, na armadura interna, o potencial:
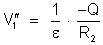
Portanto,
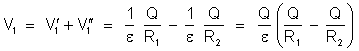
ou
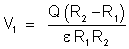
E
o potencial  vale:
vale:
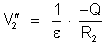
Logo,
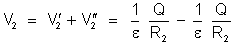
ou
Poderíamos
ter previsto que o potencial da armadura externa é nulo porque ela
está ligada à terra.
A
diferença de potencial entre as armaduras é:
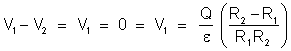
E
a capacidade do condensador:
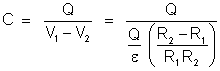
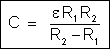
Para
que o condensador tenha grande capacidade é necessário que os raios
sejam grandes, mas a diferença entre os raios é pequena. Vemos
que a capacidade é diretamente proporcional à constante dielétrica
do isolante.

1a) Vimos
que a armadura externa tem potencial nulo. Isso acontece todas
as vezes que o induzido está ligado à terra. Baseados nesse fato,
muitos autores definem condensador do seguinte modo: condensador
é o conjunto de dois condutores separados por isolante, um dos
quais com potencial nulo.
2a) Se
a esfera A estivesse isolada de outros condutores e circundada
por um isolante de constante dielétrica  , o seu potencial seria:
, o seu potencial seria:
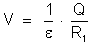
Com
a presença da esfera B, o potencial de A passa a valer  , dado por:
, dado por:
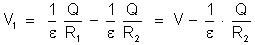
Logo,
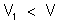
Concluímos
que a esfera A, carregada com a carga Q em presença do corpo B
ligado à terra, adquire um potencial  menor que o potencial V que ela adquire quando carregada
com a mesma carga Q, mas isolada. A capacidade de A em presença
de B é então
menor que o potencial V que ela adquire quando carregada
com a mesma carga Q, mas isolada. A capacidade de A em presença
de B é então
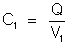
e
quando isolada é
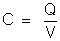
Sendo
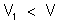 , resulta
, resulta
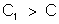
Concluímos
que, com a presença do corpo B a capacidade da esfera A aumenta.
Esse fenômeno é chamado condensação da eletricidade. Daí o nome
condensador.
Esta
2a observação serve para esclarecer melhor dois parágrafos
anteriores: o tópico "Variação
do Potencial de um Condutor sob Influência de Outro Corpo
Eletrizado",
em que estudamos a variação do potencial de um condutor pela influência
de outro corpo eletrizado, e o tópico "Capacidade
de um Condutor", em que, ao definirmos capacidade de
um condutor insistimos no fato de ele precisar estar isolado.
Pois, quando ele não está isolado, faz parte de um condensador
e a sua capacidade se modifica.

Antes
de deduzirmos a fórmula de capacidade de um condensador plano, resolvamos
o seguinte problema. Sejam dois planos paralelos, indefinidos e
muito próximos, eletrizados com densidade elétrica 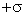 e outro com
e outro com 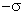 . Qual a diferença de potencial entre eles? Se os dois planos
são próximos, o campo elétrico existente entre eles é uniforme:
as linhas de força são retas e paralelas entre si, e perpendiculares
aos planos. E o vetor campo elétrico tem o mesmo módulo em todos
os pontos da região compreendida entre os planos.
. Qual a diferença de potencial entre eles? Se os dois planos
são próximos, o campo elétrico existente entre eles é uniforme:
as linhas de força são retas e paralelas entre si, e perpendiculares
aos planos. E o vetor campo elétrico tem o mesmo módulo em todos
os pontos da região compreendida entre os planos.
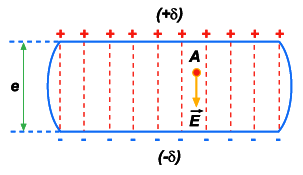

O
plano positivo produz, num ponto A qualquer, compreendido entre
os dois, um campo dirigido do positivo para o negativo, e de módulo
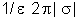 . O plano negativo produz, no mesmo ponto A, um campo também
dirigido do positivo para o negativo e de módulo
. O plano negativo produz, no mesmo ponto A, um campo também
dirigido do positivo para o negativo e de módulo 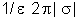 . Esses dois campos, tendo mesma direção e mesmo sentido
dão um campo resultante
. Esses dois campos, tendo mesma direção e mesmo sentido
dão um campo resultante 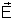 ainda de mesma direção e mesmo sentido, e de módulo igual
à soma dos módulos:
ainda de mesma direção e mesmo sentido, e de módulo igual
à soma dos módulos:
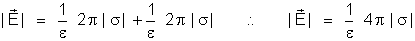
Para
calcularmos a diferença de potencial entre os dois planos, imaginemos
agora que uma carga positiva q seja deslocada do plano positivo
para o negativo. O trabalho realizado será:
Mas,
esse trabalho também é igual ao produto de força que atua na carga
pela distância e entre os planos (que é o deslocamento do ponto
de aplicação da força):
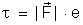
Sendo
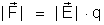
temos:
Comparando
(1) e (2), temos:
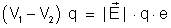
ou
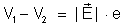
temos,
portanto :
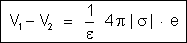

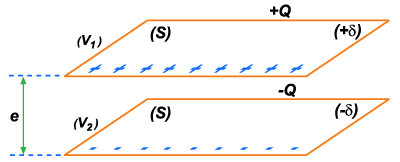
O
condensador plano é constituído por dois planos paralelos de igual
área S, separados por uma distância e muito pequena em relação a
S. Um deles recebe a carga 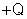 e funciona como indutor. O outro é ligado à terra e fica
com a carga
e funciona como indutor. O outro é ligado à terra e fica
com a carga 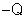 . As densidades elétricas são:
. As densidades elétricas são: 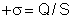 , e
, e 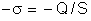 .
.
Como
a diferença de potencial entre as armaduras é dada por 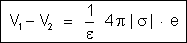 ,
a capacidade do condensador é:
,
a capacidade do condensador é:
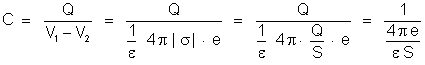
ou
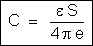
Essa
expressão mostra que para que a capacidade seja grande as armaduras
devem ter grande área S e pequeno afastamento e; e que a capacidade
é diretamente proporcional à constante dielétrica do isolante.

É
constituído por placas rnetálicas e camadas de isolante, que
se alternam. As placas metálicas de ordem par são reunidas
entre si e funcionam como uma única armadura; as de ordem
ímpar são reunidas entre si e constituem a outra armadura.
Havendo n camadas de isolante, haverá  placas metálicas. Conforme veremos
adiante, este conjunto se comporta como n condensadores
iguais ligados em paralelo. A capacidade total é igual a
n vezes a de cada um. Sendo s a área de cada placa metálica,
a capacidade de cada condensador parcial é:
placas metálicas. Conforme veremos
adiante, este conjunto se comporta como n condensadores
iguais ligados em paralelo. A capacidade total é igual a
n vezes a de cada um. Sendo s a área de cada placa metálica,
a capacidade de cada condensador parcial é: 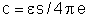 .
A capacidade total é: .
A capacidade total é:  , ou
, ou |
|
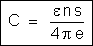
Mas,
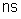 é a área total do isolante. Fazendo
é a área total do isolante. Fazendo 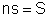 , a fórmula anterior fica
, a fórmula anterior fica
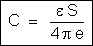
e
toma o mesmo aspecto que a fórmula 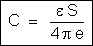 .
.
Resumindo,
podemos dizer que a capacidade de um condensador plano é sempre
calculada pela fórmula 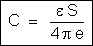 ,
seja ele um condensador simples ou de várias camadas, mas S deve
então ser considerado como a área total do dielétrico.
,
seja ele um condensador simples ou de várias camadas, mas S deve
então ser considerado como a área total do dielétrico.

É um
condensador plano de várias camadas, em que as placas metálicas
são semi-circulares dispostas de tal modo que os centros
de todos os círculos estejam sobre uma reta. As placas
de ordem par são fixas. As de ordem ímpar são presas a
uma haste metálica que passa pelos seus centros, de maneira
que, girando a haste, todas as placas de ordem ímpar giram.
Desse modo se pode modificar a área S das superfícies de
ordem par que ficam em frente às de ordem ímpar, e como
consequência a capacidade do condensador varia.
|
|

É constituída
por um frasco de vidro, que tem encaixada externamente uma
chapa metálica, e internamente, outra. A chapa interna
é a armadura indutora, a externa e a armadura induzida.
Existe uma haste metálica em contato com a armadura interna
para que ela possa ser eletrizada comodamente. Neste condensador,
muitas vezes a armadura interna, em vez de ser constituída
por uma chapa adaptada ao vidro pode ser constituída por
pedaços de metal colocados no interior da garrafa. A garrafa
de Leyden é o condensador mais antigo. Tem esse nome porque
foi inventada em 1746 na cidade de Leyden. É inteiramente
fora de uso, porque é muito incômoda.
|
|