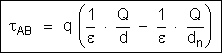
Calculemos
o trabalho realizado durante o deslocamento de uma carga dentro
de um campo elétrico. Seja o campo elétrico produzido
pela carga elétrica puntiforme Q. Uma outra carga puntiforme
q, colocada no campo, ficará sujeita a uma força
.
Se nada impedir, essa força
deslocará a carga q e realizará então um trabalho.
Calculemos o trabalho realizado pela força
para um deslocamento de q até de A um ponto B (fig. 69). Imaginemos
sempre a carga q suficientemente pequena para não alterar
o campo de Q. Quando a carga q está em A a força vale:
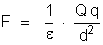
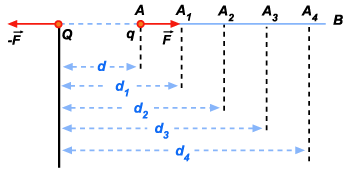
Figura 69
Mas, à
medida que a carga é deslocada, a distância d varia,
e a força também. Não podemos calcular elementarmente
o trabalho realizado por uma força variável. Por causa
disso vamos decompor a trajetória AB em número muito
grande de partes AA1, A1A2,
A2, A3,
etc., sendo essas partes suficientemente pequenas para que possamos
admitir a força como constante dentro de cada uma delas.
Assim, entre A e A1 admitamos a
força constante e com valor que ela possui em A. O trabalho
realizado entre A e A1 será:
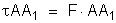
Sendo d1
a distância de A1 à
carga Q, temos
.
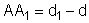Substituindo os valores de F e
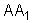em
,
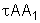fica:
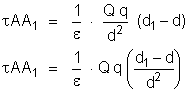
Como admitimos
A e A1 muito próximos, as
distâncias de d1 são
quase iguais. Podemos então fazer
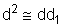e substituir, na equação de
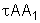o valor d2 pelo produto dd1.
Fica:
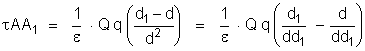
ou
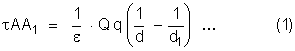
Chamamos
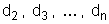respectivamente às distâncias dos pontos
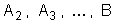até a carga , e repetindo o raciocínio para os trabalhos
realizados nos trechos
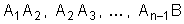encontraremos as seguintes expressões para esses trabalhos:
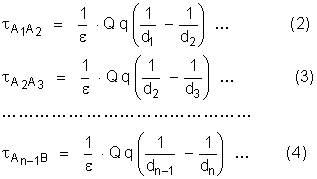
O trabalho total
entre A e B é a soma desses trabalhos parciais:
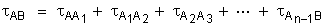
Somando membro
a membro as expressões (1), (2), (3), (4) e colocando em
evidência
,
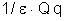temos:
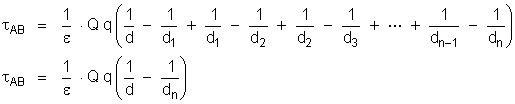
ou
