Suponhamos que
o ponto esteja infinitamente afastado, isto é,
tende para o infinito. A expressão que calculamos dará
então o trabalho que a força eletrostática
F realiza para deslocar a carga puntiforme q do ponto A ao infinito.
Nesse caso,
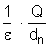
se anula, e
resulta:
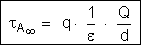
Como as expressões
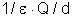e
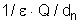tem o mesmo sinal, quando
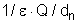é nulo a diferença entre elas é máxima.
Isso corresponde ao caso que estamos examinando. Concluímos
que o trabalho realizado quando a carga q é deslocada do
ponto A ao infinito é o máximo trabalho que se pode
obter a partir do ponto A. Esse trabalho máximo representa
a energia potencial da carga q quando ela é colocada em A,
pois a energia potencial em certa posição representa
o máximo trabalho que se pode extrair a partir dessa posição.
Concluímos que a expressão da energia potencial da
carga puntiforme q, quando ela está no ponto A, é:
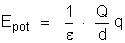
considerando
a carga como a unidade de carga, a energia potencial dessa unidade
de carga será então numericamente igual a
.
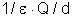Significa que o número que mede o produto
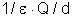é o mesmo número que mede a energia potencial da unidade
de carga. Por causa disso, a expressão A é chamada
potencial do ponto
.
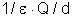Podemos então dar a seguinte definição: dada
uma carga elétrica puntiforme Q em um meio de constante dielétrica
,
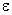chama-se potencial de um ponto situado à distância
d da carga, ao produto
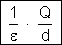
Em Física,
dizemos que uma grandeza é infinitamente grande quando ela
é muito grande em relação ao problema considerado.
Assim, dizer que
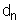tende para o infinito significa que é uma distância
muito grande em relação à extensão do
campo elétrico da carga Q. Por exemplo, suponhamos que o
campo elétrico da carga Q termine a 5 centímetros
dessa carga. Então todos os pontos que distam de aproximadamente
5 centímetros da carga Q são pontos infinitamente
afastados da carga, se os considerarmos como pontos do campo elétrico
dessa carga. Embora em outros problemas a distância de 5 centímetros
possa ser muito pequena, no caso do campo elétrico citado
ela não é pequena. Em resumo, pontos infinitamente
afastados de uma carga elétrica são pontos que estão
nos fins do campo dessa carga.
Fazendo um
resumo do que dissemos acima sôbre potencial, podemos dizer
o seguinte: o potencial de um ponto de um campo elétrico
é a energia potencial da unidade de carga colocada nesse
ponto. Ou, em outras palavras: é o trabalho realizado pela
força eletrostática quando desloca a unidade de carga
desse ponto ao fim do campo.
Em geral representamos
o potencial pela letra v.
Na fórmula
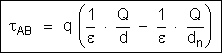que dá
,
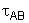temos:
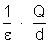
é o potencial
do ponto A, que chamaremos
;
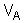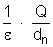
é o potencial
do ponto B, que chamaremos VB.
A fórmula
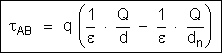pode então ser escrita:
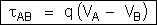
Essa fórmula
exprime o seguinte teorema: “o trabalho realizado pela força
eletrostática quando desloca uma carga elétrica puntiforme
entre dois pontos de um campo elétrico é igual ao
produto da carga pela diferença de potencial entre os dois
pontos”.
1a)
O potencial definido pela expressão
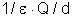é uma grandeza algébrica: pode ser positivo
ou negativo. Sempre tem o sinal da carga Q.
2a) A expressão
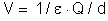mostra que, para o mesmo ambiente (mesmo
)
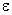e mesma carga Q, o potencial do ponto depende unicamente de
d, isto é, da posição do ponto. Por isso
dizemos que o potencial é uma função
de ponto, ou função de posição.
3a) Observemos que o potencial é inversamente proporcional
à constante dielétrica do meio.
4a) O potencial do ponto vale
.
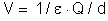O valor absoluto do potencial será:
 .
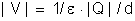O módulo do campo no ponto vale:
 .
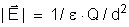Comparando as duas expressões concluímos que:
|
Suponhamos
o campo elétrico criado pelas cargas puntiformes
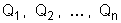(fig. 70) e um ponto A situado às distâncias
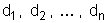dessas cargas. Chama-se potencial do ponto A, por definição,
à soma algébrica dos potenciais que as cargas produzem
separadamente em A. Isto é, por definição:
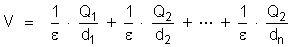(Soma algébrica)
ou
(Soma algébrica)
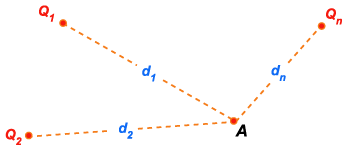
Figura 70
