
O teorema de
Gauss e o de Coulomb são dois dos mais importantes da Eletricidade.
Veremos agora uma aplicação interessante de ambos
para o estudo do campo elétrico produzido por um condutor
esférico. Seja uma esfera de raio R e carga Q (fig. 68). Um ponto pode
ocupar, relativamente à esfera, três posições:
ou é interno, ou pertence à esfera, ou é externo.
Calculemos o campo elétrico em cada um desses casos.
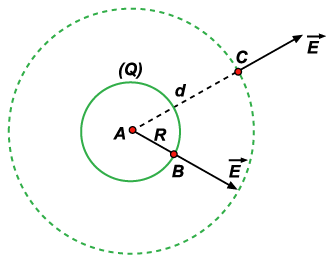
Figura 68
1o
caso) Ponto A interno – Foi provado, no tópico
"Campo
no Interior de um Condutor" , que o campo
é nulo neste ponto.
2o
caso) Ponto B pertencente à esfera – Pelo
teorema de Coulomb, em um ponto infinitamente próximo de
um condutor fechado o campo vale :
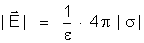
Esse também
é o campo em um ponto da própria superfície
do condutor. Tratando-se de uma esfera, a área vale:
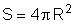 .
Então:
.
Então:
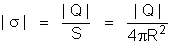
Fica:
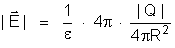 ou
ou
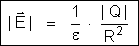
3o
caso) Ponto C externo – Seja d a distância
de C ao centro da esfera. Consideremos uma superfície esférica
imaginária de raio d concêntrica à esfera
de raio R. Como há uma simetria, o campo elétrico
em todos os pontos dessa superfície tem o mesmo módulo
 .
O fluxo através dessa superfície é então,
em módulo:
.
O fluxo através dessa superfície é então,
em módulo:
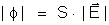
Mas,
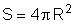 .
Então:
.
Então:
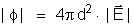
A carga Q, que
se encontra distribuída sobre a esfera de raio R, é
interna a essa esfera de raio d. Aplicando o teorema de Gauss para
o fluxo que atravessa a superfície imaginária, temos:
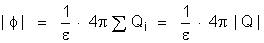
Então:
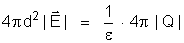
de onde:
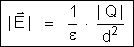
As expressões
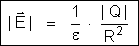 e
e
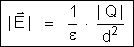 mostram que o campo produzido na superfície ou num ponto
externo de uma esfera pode ser calculado admitindo-se que a carga
da esfera seja puntiforme e colocada no centro da esfera, em vez
de estar distribuída pela superfície. Pois essas expressões
dão o módulo do campo produzido por uma carga puntiforme
Q, num meio de constante dielétrica
mostram que o campo produzido na superfície ou num ponto
externo de uma esfera pode ser calculado admitindo-se que a carga
da esfera seja puntiforme e colocada no centro da esfera, em vez
de estar distribuída pela superfície. Pois essas expressões
dão o módulo do campo produzido por uma carga puntiforme
Q, num meio de constante dielétrica
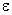 ,
em pontos situados, respectivamente, às distâncias
R e d (veja fórmula
,
em pontos situados, respectivamente, às distâncias
R e d (veja fórmula
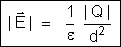 ).
).