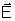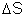Calculemos o campo elétrico em um ponto muito proximo da superfície de um condutor fechado. Consideremos um elemento de superfície do condutor de área e densidade elétrica . A carga elétrica contida em vale: .

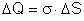Consideremos um cilindro determinado por:

a) o tubo de força determinado por ;
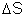b) um plano paralelo a 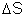e passando por ;
c) um plano paralelo a 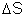e interno ao condutor.

Figura 64

Esse cilindro é uma superfície fechada. Podemos então aplicar o teorema de Gauss, para o fluxo que atravessa a superfície do cilindro:

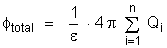
Mas, dentro desse cilindro só existe , contida em 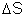, isto é,

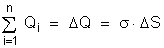
Então, em módulo:

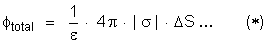
O fluxo total é a soma de três fluxos.

a) Fluxo através de CD. Sendo 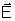o campo em A, esse fluxo vale: . .
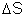b) Fluxo através de GF. É nulo, porque GF é interno ao condutor, e, no interior do condutor o campo é nulo.
c) Fluxo através da parede lateral do cilindro. É nulo, porque essa parede lateral é formada por linhas de força, que são tangentes ao campo. Então,

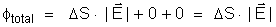
Comparando com (*), temos:

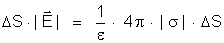
ou

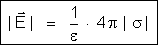
Essa expressão é o “teorema de Coulomb”: a intensidade do campo elétrico em um ponto infinitamente próximo de um condutor fechado vale , em que 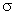é a densidade elétrica nos pontos do condutor próximos do ponto considerado.