No interior de um condutor o campo elétrico é sempre nulo.

Faremos a demonstração para o caso particular de uma esfera eletrizada. Neste caso a demonstração é simples, porque uma esfera é sempre uniformemente eletrizada, isto é, a densidade elétrica superficial é constante.

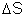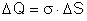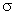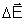Consideremos um elemento de superfície muito pequeno, de Área . . Esse elemento contém uma carga elétrica , que vale: , em que é a densidade elétrica da esfera. Em um ponto interno qualquer P a carga produz um campo cujo módulo vale (fórmula )

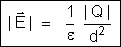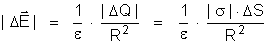
em que R é a distância 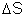de ao ponto P.

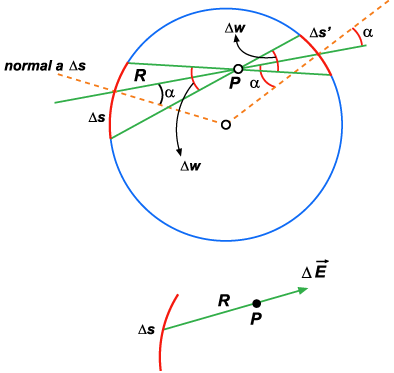
Figura 63

Mas, 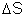e o ponto P determinam um ângulo sólido 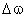. Sendo o ângulo que a normal a 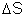faz com (a normal é o próprio raio da esfera), 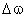vale (fórmula 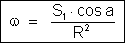na Introdução):

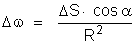
de onde:

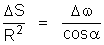
Substituindo em 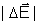, temos:

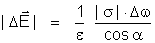
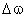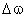Os prolongamentos das semi-retas que determinam formam um outro ângulo sólido, oposto pelo vértice de , e, portanto, igual a . Esse ângulo sólido determina, no outro lado da superfície esférica, um elemento de área 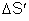, que dista de 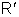do ponto . A normal a 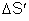faz com 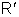um ângulo igual a 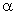(esse ângulo vale 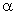porque o triângulo ABO é isósceles). Podemos então escrever que:

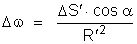
de onde

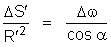
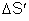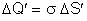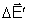Em há uma carga elétrica . Essa carga produz em P um campo , cujo módulo é:

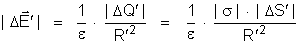
ou

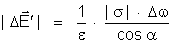
Comparando 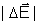com 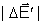vemos que são iguais. E como os dois campos, 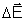e 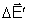, tem mesma direção e sentidos opostos, eles se anulam. O mesmo raciocínio se aplica a qualquer outro elemento 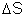da superfície da esfera: sempre há um outro elemento 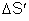cujo campo anula o campo produzido por 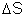. Por causa disso o campo resultante em será nulo.