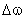Este teorema se refere ao fluxo através de uma superfície fechada, no caso em que o campo elétrico é produzido por cargas colocadas no interior da superfície. Suponhamos inicialmente uma só carga Q puntiforme colocada dentro da superfície. Consideremos na superfície um elemento de área muito pequena. Esse elemento e o ponto ocupado por determinam um ângulo sólido também pequeno.

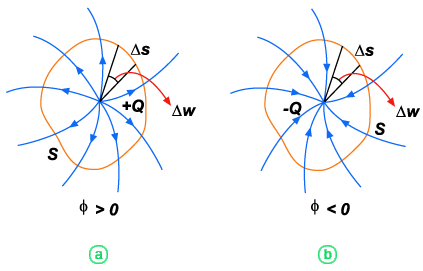
Figura 62

De acordo com o que vimos no tópico " Fluxo Elétrico do Campo Produzido por Carga Puntiforme, Através de Superfície Pequena ", o elemento de superfície é atravessado por um fluxo cujo valor absoluto é:

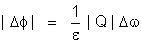
O fluxo total, através de toda a superfície, valerá a soma de todos os fluxos 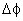considerados através de todos os elementos de superfície. Portanto,

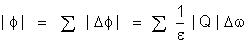
Sendo 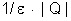constante, podemos colocar em evidência:

Mas, 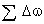representa o ângulo sólido total ao redor de um ponto. Então 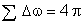esferadianos. Fica

Essa igualdade foi demonstrada para valores absolutos. Provemos que o sinal do primeiro membro coincide sempre com o do segundo. Suponhamos Q positivo; então as linhas de força “saem” de Q, e, portanto, saem da superfície (fig. 62). Mas, nós convencionamos no parágrafo anterior que quando as linhas de força saem de uma superfície fechada o fluxo que atravessa a superfície seja positivo. Logo, quando Q é positivo, 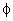também é positivo.

De igual modo se prova que quando Q é negativo, 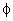também é negativo (fig. 62-b). Considerando os sinais de Q e de 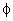a última fórmula pode ser escrita:

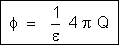
Figura 62

Suponhamos agora que, em vez de uma só carga 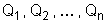, sejam colocadas no interior da superfície várias cargas . Cada uma delas produzirá um fluxo. O fluxo total será a soma algébrica dos fluxos que elas produzem separadamente:

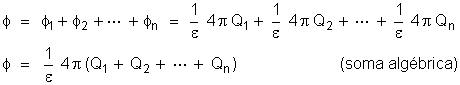
ou

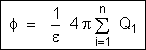
onde 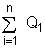representa a soma algébrica das cargas internas àsuperfície.
O teorema de Gauss pode então ser enunciado da seguinte maneira: “o fluxo total através de uma superfície fechada, e produzido pelas cargas internas é igual ao produto de 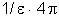pela soma algébrica das cargas internas” .