Suponhamos uma linha fechada ABCD não plana e um ponto P fora dessa linha. Imaginemos todas as retas que passam por P e pelos pontos de ABCD. Chama-se ângulo sólido à região determinada por essas retas. O ponto P é chamado vértice do ângulo sólido. Exemplo: um cone é a representação de um ângulo sólido.

Suponhamos que sejam traçadas várias esferas de centro P e raios quaisquer R , R ', R '', .... O ângulo sólido determina nessas esferas superfícies de áreas respectivamente iguais a S , S ', S '', .... Existe um teorema de Geometria que demonstra o seguinte: para o mesmo ângulo sólido é constante o quociente dessas superfícies esféricas S , S ', S '', ... pelos quadrados dos raios correspondentes. Isto é:

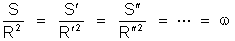
constante para o mesmo ângulo sólido.

Concluímos que esse número 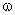obtido por qualquer um desses quocientes é uma característica do ângulo sólido. Por causa disso ele é tomado como medida do ângulo sólido.

Sendo R o raio de uma esfera qualquer de centro P, e S a área determinada nessa esfera pelo ângulo sólido, este é então medido pelo quociente:

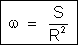
Embora esse número 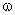seja um número abstrato, isto é, o quociente S/R² não tem dimensões físicas, nós usamos uma unidade para ângulo sólido. Essa unidade é obtida fazendo-se S = 1 e R = 1. A unidade é chamada esferoradiano, ou esferadiano; logo, um esferadiano é o ângulo sólido que, seccionado por uma esfera de raio unitário, determina nessa esfera uma superfície de área unitária.

.Nota: Esse processo usado para a medida de um ângulo sólido é idêntico ao que se usa em Geometria Plana para a medida de um ângulo plano. Dado o ângulo BAC, traçamos uma circunferência de centro A e raio R qualquer. O ângulo determina na circunferência um arco BC de comprimento . Como, para um mesmo ângulo, é constante o quociente / R, tomamos esse quociente para a medida do ângulo. Êsse quociente é também um número abstrato, mas adotamos uma unidade para a medida dos ângulos por esse processo: é o radiano. O radiano é definido como um ângulo que, seccionado por uma circunferência de raio unitário, determina nessa circunferência um arco de unidade de comprimento. Assim se o quociente / R for um número a, dizemos que o ângulo BAC tem a radianos. E escrevemos:

ou

1. O ângulo sólido compreende todo o espaço.

Nesse caso, seccionado por uma esfera, determina sobre ela toda a superfície da esfera, isto é, 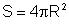. A medida desse ângulo sólido será:

2. O ângulo sólido é muito pequeno.

Nesse caso, a intersecção com a esfera pode ser confundida com uma superfície plana ABC tangente à esfera num ponto O. O raio R que passa por O é perpendicular a essa superfície plana. Sendo S a área dessa superfície plana, a medida do ângulo sólido pode ser tomada como

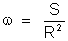
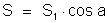
Se traçarmos uma outra superfície plana A1BC1, não perpendicular ao raio R, desde que o ângulo sólido seja muito pequeno, podemos considerar a superfície ABC como a projeção de A1BC1 sobre um plano perpendicular a R. Então sendo S1 a área de A1BC1 e a o ângulo formado pelas duas superfícies, que é também o ângulo formado pelas duas normais às superfícies, temos pela fórmula: Podemos então medir o ângulo sólido a partir dessa supefície A1BC1 substituindo, na expressão de 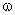, o valor S por . 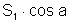Fica:

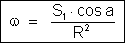
Esse é o valor de um ângulo sólido pequeno expresso em função da área de uma superfície plana qualquer seccionada pelo ângulo, da distância R do vértice do ângulo ao centro dessa superfície, e do coseno do ângulo que R faz com a normal à superfície.