As grandezas físicas dividem-se em dois grupos:

Grandeza escalar

Grandeza escalar é aquela que fica perfeitamente determinada quando conhecemos o seu significado físico e o número que a mede. Êsse número depende da unidade escolhida para a medida da grandeza. Por exemplo: uma densidade se caracteriza por ser o quociente da massa por volume; e fica determinada quando conhecemos o número que a mede. Suponhamos que a densidade de um corpo seja 2 g/cm³; o número que a mede é 2. Mas , se mudarmos a unidade para kg/cm³, o número que a mede passará a ser 0,002, porque 1 g/cm³ = 0,001kg/m³.

Grandeza vetorial

Grandeza vetorial é aquela que não fica perfeitamente determinada só pelo significado físico e um valor numérico, porque possui, além desses dois elementos, uma direção e um sentido. É o caso de uma velocidade, por exemplo. Fisicamente a velocidade significa um quociente de espaço por tempo. Suponhamos que uma velocidade valha 5 m/seg (ou 500 cm/seg). Para que ela seja uma grandeza física perfeitamente conhecida não basta sabermos que se trata de um quociente de um espaço por um tempo e que vale 5 (ou 500). Pois um móvel, dotado de uma velocidade de pode estar se deslocando no espaço em uma infinidade de direções e de sentidos. Para que conheçamos exatamente a velocidade desse móvel precisamos saber em que direção e em que sentido ele se desloca à razão de 5 metros por segundo.

Portanto, uma grandeza vetorial se caracteriza por quatro elementos: significado físico, valor numérico (módulo), direção e sentido. É o que acontece, por exemplo, com velocidade, força, aceleração, etc..

Notamos que o significado físico é aquilo que a grandeza representa dentro da Física. Enquanto que o valor numérico, a direção e o sentido são as características matemáticas da grandeza (e não características físicas). Ao conjunto dessas três características puramente matemáticas da grandeza vetorial chamamos vetor.

Portanto, chama-se vetor ao conjunto do valor numérico, direção e sentido. É um ente puramente matemático, sem qualquer significado físico.

Chama-se módulo de um vetor ao seu valor numérico.

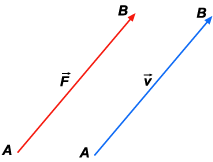
É preciso distinguir o vetor da grandeza vetorial. Esta possui um significado físico. O vetor não possui. Assim, duas grandezas vetoriais diferentes podem ter o mesmo valor numérico, a mesma direção e o mesmo sentido. Por exemplo: uma força pode ter módulo 2, direção AB e sentido de A para B. Uma velocidade, que é uma grandeza diferente de uma força, pode ter o mesmo módulo 2, a mesma direção AB e o mesmo sentido de a para B . Logo o vetor correspondente a essas duas grandezas vetoriais é o mesmo, embora elas sejam grandezas de espécies diferentes; isto é, essas duas grandezas são diferentes sob o ponto de vista físico, porque uma é força e outra é velocidade, mas têm as mesmas características matemáticas.

Sob o ponto de vista da Matemática, é muito cômodo estudarmos as operações com vetores, isto é, exclusivamente com módulo, direção e sentido, independentemente do significado físico, pois assim o cálculo pode ser aplicado a qualquer grandeza vetorial, qualquer que seja o seu significado físico. A parte da Matemática que estuda essas operações é chamada Cálculo Vetorial.

Um vetor é representado por um segmento de reta orientado que tenha a direção e o sentido do vetor, e comprimento igual ao módulo do vetor (segmento de reta orientado é aquele no qual estabelecemos um sentido de percurso). Indica-se um vetor com uma letra encimada por uma flecha: , , 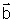, , 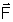, 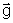etc..

Dois segmentos de reta orientados são chamados equipolentes quando têm mesmo módulo, mesma direção e mesmo sentido. Concluímos que diversos segmentos de reta equipolentes representam o mesmo vetor. Estudaremos um resumo das seguintes operações vetoriais: adição, decomposição, subtração, multiplicação de um vetor por um número, divisão de um vetor por um número.

Suponhamos dois vetores 1 e 2 representados pelos segmentos orientados AB e CD. Podemos representar o vetor por um segmento AE equipolente a CD, tomado a partir de A (figura abaixo). Sobre os segmentos AB e AE construamos um paralelogramo ABFE, e consideremos a diagonal AF como um segmento orientado de A para F. Essa diagonal representará então um vetor . Esse vetor é chamado soma de 1 e 2 . Escrevemos = 1 + 2

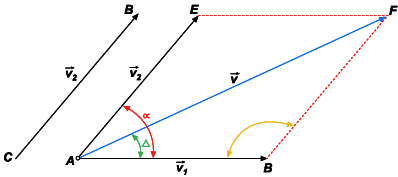
Chama-se soma de dois vetores e ao vetor representado pela diagonal do paralelogramo construído sobre os segmentos que representam e .

Módulo da soma

Pode ser calculado pela lei do coseno, que diz: "em qualquer triângulo, o quadrado de um lado é igual à soma dos quadrados dos outros dois lados, menos o duplo produto desses dois lados pelo coseno do ângulo que eles formam".
Aplicando a lei ao triângulo ABF, temos:

Mas:

Fica:

Sendo o ângulo formado por ₁ e ₂ temos:

A expressão anterior fica:

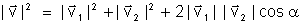
Direção da soma

Pode ser assinalada por meio do ângulo que a soma faz com um dos vetores dados. Por exemplo, pelo ângulo que faz com . Aplicando ao triângulo ABF a lei dos senos que diz: "em qualquer triângulo é constante o quociente de cada lado pelo seno do ângulo oposto", temos:

Mas

.

Substituindo esses valores resulta:

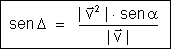
Sentido da soma

Não podemos exprimir algebricamente o sentido da soma.

Observação

Baseado nesse caso geral, o leitor pode verificar facilmente os casos particulares seguintes. 1o - Os dois vetores tem mesma direção e mesmo sentido; a soma terá mesma direção, mesmo sentido, e por módulo a soma dos módulos. 2o - Os dois vetores tem a mesma direção, mas sentidos opostos. O vetor soma terá ainda a mesma direção; terá o sentido do vetor de maior módulo; e por módulo, a diferença entre os módulos.

É a operação inversa da soma. Dado um vetor , decompô-lo em dois outros, ₁ e ₂, é determinar dois vetores ₁ e ₂ que somados dem .

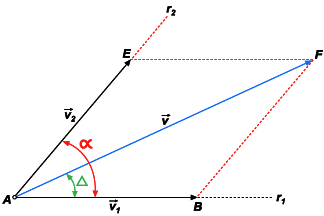
Há uma infinidade de pares de vetores ₁ e ₂ que somados dão , isto é, o problema da decomposição tem uma infinidade de soluções. Mas, o caso mais comum é aquele em que são fixadas as direções de ₁ e ₂, e então o problema passa a ter uma única solução. Suponhamos que os vetores ₁ e ₂ devam ter as direções das retas r₁ e r₂. Por F traçamos a reta FB paralela a r₂, que determina em r₁ o segmento AB, e FE paralela a r₁, que determina em r₂ o segmento AE. Os vetores ₁ e ₂ são os procurados.

Num caso de decomposição podemos usar as mesmas fórmulas 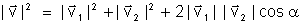e 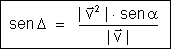que no caso da soma, com a diferença de que, na decomposição, deixa de ser incógnita.

Chama-se vetor oposto de um vetor dado a um outro vetor que tenha igual módulo, mesma direção e sentido oposto ao do vetor dado. O oposto de um vetor representa-se por - :

Chama-se diferença de um vetor e um , à soma de com o oposto de: Escreve-se = 1 - 2 ; de acordo com a definição, 1 - 2 = 1 + (- 2) Como a subtração recai num caso de soma, podemos aplicar aqui o que foi visto para a soma.

Suponhamos dados um vetor e um número m. Por definição, chama-se produto do vetor pelo número m, a um vetor a que tem:

por módulo, o produto de m pelo módulo de ; por direção, a direção de ; por sentido, o sentido de , quando m é positivo, e contrário ao de , quando m é negativo.

Por definição, chama-se quociente de um vetor por um número m, a um vetor que tem:

por módulo, o quociente do módulo de por m; por direção, a direção de ; por sentido, o sentido de , quando m é positivo, e contrário ao de , quando m é negativo.

Autor: Roberto A. Salmeron