Após a abordagem inicial realizada por Fresnel, um tratamento matemático mais preciso do princípio de Huygens foi proposto por Kirchhoff, da forma como segue. Vamos partir da segunda identidade de Green, que é expressa como:

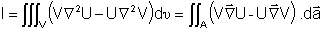
onde U e V são funções contínuas e integráveis que obedecem a equação de ondas:

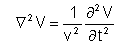
Note que o meio é homogêneo, logo v não depende de r. As soluções da equação de ondas são da forma:

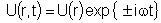
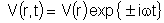
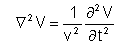que quando substituídas nas equações e resultam em:

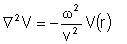
Com isto notamos que o integrando do lado esquerdo da eq. 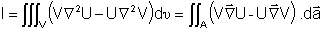é nulo, isto é,

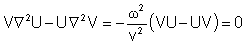
Assim, A superfície fechada A envolve o volume de interesse, que podemos tomar como sendo aquele da Fig. 9.4. Neste caso, podemos dividir a integral em duas regiões, S₁ e S₂, tal que: .

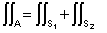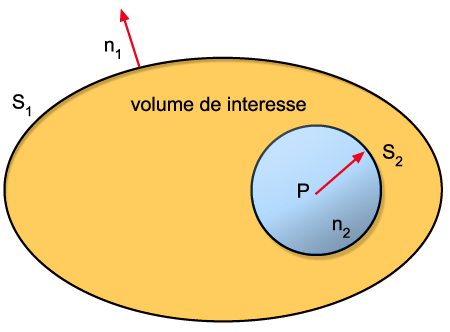
Fig. 9.4 - Geometria utilizada para o cálculo da integral de superfície

Queremos encontrar o valor da função U no ponto de observação P e para isto tomaremos V(r,t) como sendo uma onda esférica da forma O gradiente em coordenadas esféricas é dado por:

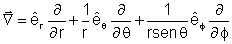
de forma que a integral de superfície em S₂ fica:

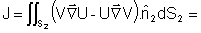
onde , que substituidos na eq. resulta em:

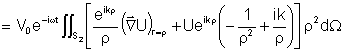
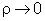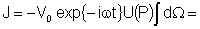
Tomando o limite obtemos 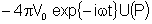. Logo, 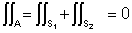como temos:

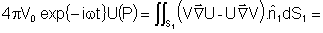
que nos leva à equação básica da teoria da difração:

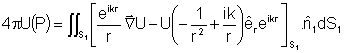
Esta expressão é chamada de teorema integral de Kirchhoff. Ela relaciona o valor da função no ponto de observação P com valores desta função e sua derivada sobre a superfície S₁ que envolve o ponto P. Como tomamos 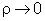, a Fig. 9.4 se modifica da maneira mostrada na Fig. 9.5. Particularizando a eq. 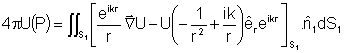para o caso em que U é também uma onda esférica da forma:

o teorema integral de Kirchhoff pode ser escrito de forma mais explícita como:

Fig. 9.5 - Geometria usada no cálculo da integral Kirchhoff.

Nos fenômenos de difração r₁ e r₂ são geralmente grandes, de forma que podemos desprezar o segundo termo. Assim obtemos:

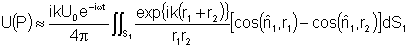
Esta é a conhecida fórmula de Fresnel-Kirchhoff. Vamos especializá-la para o caso de difração por uma fenda de área A, na geometria da Fig. 9.3, com S₁ = S’+ A. Pode-se mostrar que a integral sobre S’ é desprezível e assim,

onde ( 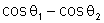) é chamado de fator de obliquidade. A fórmula de Fresnel-Kirchhoff nada mais é do que a afirmação matemática do princípio de Huygens. Para examinar melhor este ponto vamos tomar uma abertura circular com a fonte S localizada no eixo de simetria da abertura conforme mostra a Fig. 9.6. A superfície de integração A é um pedaço de casca esférica de raio r₁ e centro S de forma que 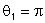. Logo:

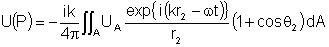
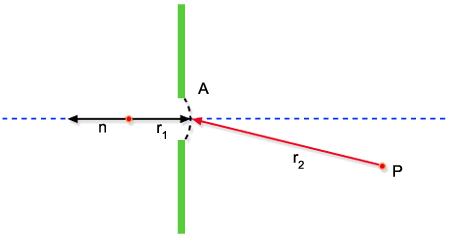
Fig. 9.6 - Difração em uma fenda circular.

onde é a amplitude da onda primária incidente. A partir dela, cada elemento dA da abertura gera uma onda esférica secundária . No princípio de Huygens não existe o fator de obliqüidade nem a fase introduzida no campo pela difração. Note que a difração na direção da fonte é zero pois 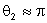e o fator de obliqüidade é nulo.

Sergio Carlos Zilio