Levando em conta a natureza ondulatória da luz, que será discutida no próximo capítulo, podemos explicar como se processa o efeito de focalização produzido por uma lente fina de índice de refração n. Consideremos uma onda colimada que se propaga para a direita e incide sobre uma lente compreendida entre dois planos muito próximos como apresentado na Fig. 3.7. Esta onda “plana”, que analisaremos mais detalhadamente na seção 4.3, é caracterizada por uma fase espacial dada por f = kz, onde z é direção de propagação e k = 2p/l. Ao atravessar a lente, haverá uma mudança de fase da onda, que depende da distância r, relativa ao centro da lente. Tal mudança é dada por Df = k₀D(r), onde k₀é o vetor de propagação no vácuo e D(r) é o caminho óptico, já definido quando tratamos do princípio de Fermat. Com base na Fig. 3.7, e denominando de d a espessura da lente, encontramos que o caminho óptico entre os planos 1 e 2 é dado por:

onde n₀é o índice de refração do ar, que doravante tomaremos como unitário (n₀=1). As distâncias d₁ e d₂ entre a lente e os planos 1 e 2 podem ser calculadas através de argumentos geométricos, levando em conta que cada superfície da lente tem formato esférico. Assim, para a primeira superfície,

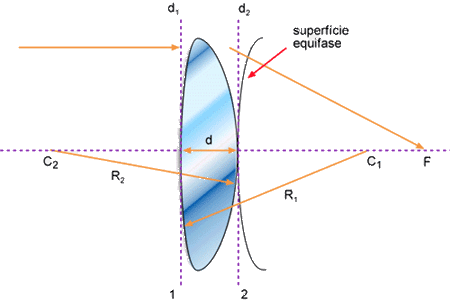
Fig. 3.7 – Geometria utilizada para o cálculo da mudança de fase
de uma onda plana após a passagem por uma lente fina.

onde 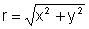e a coordenada transversal a z. Expandindo o quadrado e supondo que d₁é muito menor que R₁ e r, obtemos:

(3.25a)

Procedendo de forma análoga para a superfície de raio R₂ temos:

(3.25b)

de forma que o caminho óptico é dado por:

(3.26)

onde a equação do fabricante de lente, eq. (3.12), foi utilizada nesta última passagem. Como consequência, a fase da onda sobre o plano 2 é:

(3.27)

onde no primeiro termo da direita subtraimos a quantidade k₀d, que é a fase que a onda ganharia se não houvesse lente. S(r,z) é a função eikonal, que foi introduzida na eq. (2.38). Tomando o gradiente de S(r,z) em coordenadas cilíndricas podemos encontrar o versor û, paralelo a 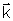, que define a direção de propagação da onda. Assim, de acordo com a eq. (2.41) temos:

(3.28)

mostrando que a luz convergirá para o ponto focal F, pois tgq = r/f. Em outras palavras, a ação da lente é a de produzir uma curvatura na frente de onda. A fase diminui radialmente sobre o plano 2 e para termos uma superfície equifase teremos que caminhar para a direita conforme r aumenta. Assim o termo k₀z compensa o decréscimo radial da fase.

Sergio Carlos Zilio