Ao tratarmos o tópico óptica de raios, também conhecido como óptica geométrica, não levamos em consideração o caráter ondulatório da luz, nem sua polarização. Nestas condições, efeitos tais como difração e interferência não se evidenciam. 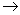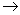Como veremos adiante, isto corresponde ao caso em que o comprimento de onda tende a zero ( l 0), que é análogo ao limite clássico que se obtém da mecânica quântica ao tomarmos h 0 . Este raciocínio foi utilizado por Schrödinger na obtenção da sua famosa equação, como mostraremos no final do capítulo.

Entende-se como meio homogêneo aquele no qual o índice de refração não depende da posição, sendo portanto constante. Note que o meio pode ser simultaneamente homogêneo e anisotrópico, caso comum em cristais, para os quais o índice de refração tem valores diferenciados para distintas direções de propagação da luz. Já no meio não homogêneo, o índice de refração é dependente da posição, em geral devido às flutuações de densidade, temperatura, ou composição química do material.

Este capítulo inicia-se com uma breve exposição das propriedades de propagação de raios em meios homogêneos, com ênfase na sua refração ao atingir uma interface dielétrica plana. Este é um tópico que será revisto no Cap. 6, depois que abordarmos os conceitos de polarização da luz e condições de contorno do campo eletromagnético, que nos levarão às equações de Fresnel. Em seguida, trataremos de uma situação bem mais interessante, a propagação de luz em meios não homogêneos. Mostraremos que a trajetória dos raios de luz podem descrever uma trajetória curva, diferentemente dos meios homogêneos, onde as trajetórias dos raios são retilíneas. Serão apresentados quatro tratamentos teóricos para este tipo de problema. Em particular, faremos, no final do capítulo, uma analogia entre a mecânica clássica e a óptica geométrica. Esta analogia será importante para a obtenção da equação de Schrödinger.

A área de óptica é um campo de estudos fascinante. De maneira simplificada, podemos dizer que ela é o ramo da Física que estuda a propagação da luz e sua interação com a matéria. Em muitas áreas da ciência e tecnologia, o entendimento de determinados conceitos pode ser difícil porque seus efeitos não são facilmente visualizados. Na óptica, entretanto, o simples uso de um laser permite a visualização de um dado efeito como função de vários parâmetros, facilitando o aprendizado. Isto se deve principalmente à coerência, monocromaticidade e colimação da luz proveniente deste instrumento, que permitem a observação de fenômenos tais como interferência e difração, nos quais a natureza ondulatória da luz se manifesta claramente. Entretanto, para se chegar ao desenvolvimento deste dispositivo, e de vários outros que são importantes no nosso cotidiano, um longo caminho foi percorrido e este percurso gerou um histórico bastante rico. Alguns aspectos que merecem destaque estão ligados às idéias sobre a natureza da luz e aos caminhos paralelos que a óptica e o eletromagnetismo trilharam durante séculos. Para se entender um pouco estes fatos, faremos, no transcorrer desta seção, uma breve revisão histórica do desenvolvimento dos conceitos principais ligados à óptica.

Um outro fato importante para o qual deve-se chamar a atenção refere-se à analogia existente entre a óptica física e a mecânica quântica. No estado estacionário, ambas são descritas pela mesma equação de ondas e assim, vários fenômenos que se observa num laboratório de óptica podem ser usados para um melhor entendimento da mecânica quântica. Apenas como exemplo, o princípio da incerteza de Heisenberg pode ser verificado num experimento de difração de luz por uma fenda, como veremos no Cap. 9. Similarmente, outros fenômenos nos quais a matéria comporta-se de forma ondulatória encontra seu análogo na óptica física. Desta forma, o aprendizado da mecânica quântica torna-se mais simples com o auxílio da óptica.

Sergio Carlos Zilio