|
| |
Às
vezes empregamos um sistema de espelhos. Alguns arranjos produzem
efeitos deveras interessantes. Com eles podemos obter muitas imagens
de um objeto, simulando situações deveras impressionantes.
Outras vezes estamos apenas interessados em construir sistemas
ópticos simples.
Consideremos dois espelhos colocados perpendicularmente um em
relação ao outro. É fácil verificar
que nesse caso são formadas três imagens. À
medida em que o ângulo aumenta, o número de imagens
diminui. Vale o contrário também. À medida
em que o ângulo diminui o número de imagens aumenta.
Uma situação curiosa é aquela na qual os
espelhos são dispostos paralelamente um ao outro. Formam-se
infinitas imagens.
Por
que as imagens se multiplicam? Isso ocorre porque algumas imagens
se transformam em objetos colocados na frente do espelho. As imagens
na frente de um espelho se comportam como objetos na frente dos
mesmos produzindo uma nova imagem. Quando a imagem de um espelho
se coloca atrás do outro espelho o processo se torna inviável
a partir desse ponto.
Quantas imagens se formarão?
Sendo 
o ângulo (medido em graus) entre os espelhos, então,
se 360/
for um número inteiro par, o número de imagens será
dado por
.
Se 360o/
for um número ímpar a expressão acima só
valeria para objetos localizados no plano bissetor de
.
No caso anterior, em que 360/
= 4 obtemos o número correto de imagens, isto é
.
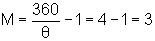Se o ângulo for 60o o número
de imagens será 5.
No
caso de dois espelhos paralelos localizados a uma distância
d o número de imagens é infinita. Isso porque cada
imagem se comporta como um objeto para o outro espelho. Temos assim
um número infinito de imagens. Tem a imagem e a imagem da
imagem e assim sucessivamente. A localização de cada
uma das imagens é muito simples.
|
|
|
