|
| |
Consideremos
um espelho plano que experimenta uma rotação de
um ângulo, digamos
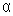 ,
por uma das suas extremidades. O que acontece nesse caso com a
imagem de um ponto P. Claramente ela muda da posição
P' de para P". A questão que se coloca é de
que quanto ela se deslocou. ,
por uma das suas extremidades. O que acontece nesse caso com a
imagem de um ponto P. Claramente ela muda da posição
P' de para P". A questão que se coloca é de
que quanto ela se deslocou.
Por se tratar de uma rotação vamos analisar o deslocamento
em termos de variáveis angulares. Para tal consideremos
um círculo com centro no ponto C que é um ponto
num eixo em torno do qual se deu a rotação do espelho,
como mostra a figura.
Olhando para
esse círculo vê-se que a imagem deslocou-se de um
ângulo
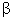 . .
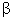 é, portanto, o deslocamento angular da imagem.
é, portanto, o deslocamento angular da imagem.
Pode-se
mostrar com base em propriedade geométrica relativamente
simples que
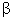 = 2
= 2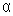
ou
seja, o deslocamento angular da imagem é duas vezes maior
do que o ângulo de rotação do espelho.
Note que o ponto C é equidistante de P1'
e de P e também de P2',
já que se trata de imagem e objeto, sendo este (o objeto)
mantido fixo. Portanto, P1', P
e P2' pertencem a uma circunferência
com centro em C.
O ângulo
P1' P P2'
= 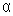 , pois P P2' é perpendicular
ao espelho na posição E2
e P P1' é perpendicular
ao esplho na posição E1.
O ângulo P1' P P2'
é inscrito na circunferência e o ângulo P1'
C P2' é central à
mesma circunferência. Os dois ângulos compreendem
o mesmo arco P1' P2'
de onde decorre que o ângulo P1'
C P2' = 2 P1'
P P2' .
, pois P P2' é perpendicular
ao espelho na posição E2
e P P1' é perpendicular
ao esplho na posição E1.
O ângulo P1' P P2'
é inscrito na circunferência e o ângulo P1'
C P2' é central à
mesma circunferência. Os dois ângulos compreendem
o mesmo arco P1' P2'
de onde decorre que o ângulo P1'
C P2' = 2 P1'
P P2' .
P1'
C P2' =
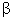
P1'
P P2' =
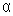 .
.
Portanto,
o deslocamento angular da imagem 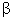 é o dobro do deslocamento do espelho
é o dobro do deslocamento do espelho 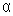 . .
Por exemplo, um motorista acerta o espelho retrovisor do carro girando-o
convenientemente. Em alguns carros o espelho é plano e em
outros é convexo. Supondo que seja um espelho plano, ao girar
o espelho muda-se o campo visual. Um ponto fixo dentro do campo
visual será vista em outra posição já
que a imagem se deslocará com a sua rotação.
|
|
|