Consideremos agora a expressão para a energia cinética do corpo rígido. Sua energia cinética é dada por

.

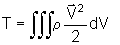
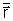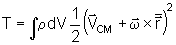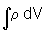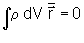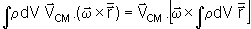
Lembrando agora que a velocidade do ponto do corpo rígido localizado na posição (em relação ao centro de massa) é dada por , segue que . Lembrando as propriedades = massa total do corpo rígido = M e e que: obtém-se .

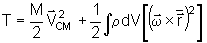E portanto, a energia cinética se constitui de duas partes. A primeira é a energia cinética de translação do corpo como um todo (é a energia cinética do centro de massa). A segunda está associada à rotação do corpo rígido.

Lembrando a identidade

.

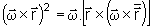
Podemos escrever T sob a forma

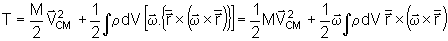
Lembrando a definição do momento angular , notamos que T pode então ser então escrito agora como

.

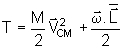
Vemos que a energia cinética de rotação é dada por

,

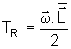
ou, de um modo equivalente,

ou ainda

.
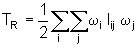