| |
O
corpo rígido é um caso particular de um sistema de N
partículas. Ele é particular no sentido de manter as
distâncias, entre as várias partes que o compõem
(átomos), invariáveis. As distâncias entre os
vários pontos do corpo rígido são fixas (só
nesse sentido a rigidez).
Qualquer
deslocamento de um ponto P do corpo rígido pode sempre ser
dado como uma soma de dois termos. Um deles associado ao movimento
de translação do corpo rígido como um todo e
o outro associado a uma rotação pura do corpo rígido.
Escrevemos, assim
.
Para
entendermos isso basta imaginarmos um sistema de referência
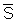solidário ao corpo rígido, com origem num ponto
O, arbitrariamente escolhido, do mesmo. A posição
de um ponto P do corpo rígido, com respeito a um sistema
de referência S, será dada por
,
onde
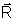é a posição do ponto O e 
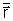o vetor posição relativa a ele.
Portanto
|
|
onde
descreve o deslocamento do ponto O do corpo e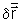 
corresponde ao deslocamento associado à rotação
em torno de O. Já vimos que
,
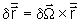onde
 
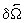é o vetor deslocamento angular. Portanto, podemos escrever
para a velocidade de um ponto do corpo rígido:
,
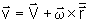
onde
é a velocidade de O.
Como
o movimento mais geral do corpo rígido consiste de um movimento
de translação e um outro de rotação, dizemos
que o corpo rígido requer seis graus de liberdade para descrevê-lo:
Translação:
3 coordenadas do ponto O.
Rotação:
3 ângulos de Euler.
|
|
