Vamos calcular o trabalho realizado por algumas das forças consideradas nos capítulos anteriores. Vamos começar pela força normal.

A força normal 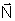é sempre perpendicular à direção do deslocamento (e do movimento). Isso significa que a projeção da força na direção de deslocamento é nula. Matematicamente,

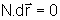
Portanto, o trabalho realizado pela força normal é nulo.

Como a força da gravidade na proximidade da terra é uma força constante m 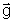, o trabalho da força da gravidade será dada por 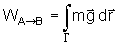. Escolhendo o eixo y de acordo com a figura ao lado verifica-se que .

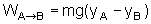Observe-se que o trabalho depende apenas da variação da altura. Isso ocorre porque deslocamentos na direção horizontal dão contribuição nula para o trabalho, pois a força de gravidade é perpendicular a esses deslocamentos.

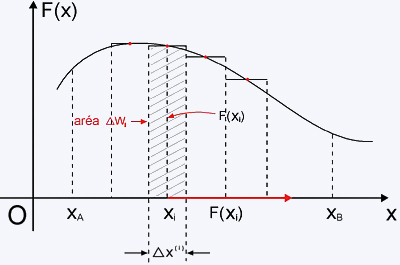
Dada uma força dependente de x, podemos dividir o deslocamento entre as posições x_A e x_B em pequenos intervalos 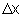. Para cada um desses intervalos aplicamos a fórmula para força constante, pois essa divisão procura justamente isso, ou seja, busca intervalos tão pequenos que para cada um deles possamos utilizar a expressão para força constante. Disso obtemos, para o i-ésimo intervalo, o trabalho

.

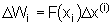valor esse igual ao da área do retângulo tracejado mostrado na figura

O trabalho total é o limite da soma

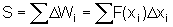
quando aumentarmos o número de divisões fazendo os 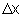_i tenderem a zero, isto é,

.

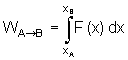O significado de 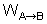é que ele é igual a área da região compreendida entre o eixo x, a curva F(x) e as verticais por x_A e x_B, considerando-se essa área negativa quando F(x) é negativa.

No caso da força elástica, F(x) = -k x, a curva F(x) é a reta , mostrada na figura abaixo. A área do triângulo tracejado é, 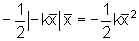. Portanto, 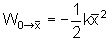. Esse resultado vale também para 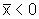pois, nesse caso,
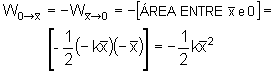