| |

Quando
definimos energia dissemos que os físicos preferem definir
Energia como a capacidade de realizar trabalho (em vez de tarefas).
Trabalho é um conceito muito abstrato (nada intuitivo, de fato)
mas que, por outro lado, introduz um rigor matemático e, portanto
precisão, na definição de energia. Para ser bem
preciso, o que se pode afirmar é que, se alguma força
realizou trabalho, então houve variação de energia.
O
trabalho aqui definido se constitui, portanto, numa medida de
quanto uma forma de energia se altera (varia) quando um móvel
se desloca de um ponto A para o ponto B. |
 |

Para uma força constante, o trabalho realizado pela força
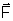 sobre uma partícula, quando esta se desloca linearmente de
A até B, é dado pelo produto escalar
sobre uma partícula, quando esta se desloca linearmente de
A até B, é dado pelo produto escalar
|
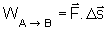
,
onde 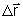 é o vetor deslocamento de A até B:
é o vetor deslocamento de A até B:
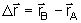
.
Portanto,
trabalho é uma grandeza escalar e seu valor é
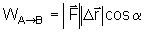
. |
|

Imaginemos que queremos calcular o trabalho de uma força 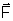 quando a partícula percorre um caminho arbitrário
quando a partícula percorre um caminho arbitrário 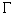 do ponto A até o ponto B.
do ponto A até o ponto B.
Agora
podemos definir o trabalho no percurso total 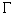 como sendo a soma em cada deslocamento parcial:
como sendo a soma em cada deslocamento parcial:
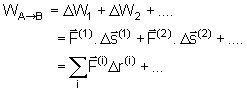
Na
verdade, esse é apenas um valor aproximado do trabalho. Para
obter o valor exato, devemos fazer o número de divisões
tender a infinito e de tal forma que as amplitudes de todos os intervalos
vão tendendo a zero. Por esse processo, a somatória
do segundo membro de (15.6) tende para um valor bem definido, indicado
com
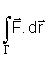
e
denominado integral de linha de um vetor 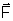 ao longo de uma curva
ao longo de uma curva 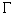 .
Assim, .
Assim,
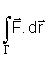 .
.
Escrevendo o deslocamento
infinitesimal ao longo da curva, 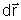 ,
na forma ,
na forma
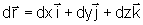 ,
,
onde
dx, dy e dz são as variações infinitesimais correspondentes
de x, y e z podemos escrever também
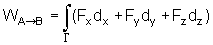 .
.
Essa
é a forma usualmente empregada no cálculo do trabalho.
|
|