| |
Nesta seção estudaremos, utilizando vetores, o movimento
de uma partícula quando esta se move sobre uma curva
específica: um carrinho transportando pessoas numa
montanha russa, por exemplo.
Como a velocidade e a aceleração são grandezas
vetoriais, procuraremos especificá-las em cada ponto
P da trajetória.
|
|
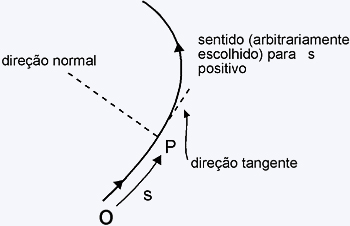
Procuraremos
definir as componentes tangente e normal da velocidade e da aceleração
em cada ponto. Num ponto arbitrário podemos introduzir uma
direção tangente e uma direção normal
à curva nesse ponto.
Assim, podemos definir a componente tangente da velocidade e da aceleração
como sendo a projeção da velocidade e da aceleração
na direção tangente à curva. Essas componentes
são exatamente o que denominamos antes de velocidade e aceleração
escalar:
Como
o vetor velocidade é sempre tangente à trajetória,
a componente da velocidade na direção normal é
nula, isto é,
vn = 0.

No entanto, a
aceleração tem uma componente normal apontando para
dentro da curva, dada por
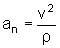
onde 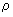 é o raio de curvatura no ponto P.
é o raio de curvatura no ponto P.
Para especificarmos o raio de curvatura, introduzimos uma circunferência
tangente à curva pelo ponto P (circunferência
osculadora). A maneira de construí-la é a seguinte:
Consideremos, além do ponto P, mais dois outros pontos P1 e P2 ao longo da curva.
Por esses três pontos (isso vale para quaisquer três pontos
não alinhados) podemos fazer passar uma circunferência.
Ao tomarmos P1 e P2
cada vez mais próximos de P, definimos a circunferência
osculadora, passando por P. Essa circunferência tem um raio
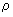 . .

Gil Marques
|
|