| |
Se
a velocidade de um objeto varia com o tempo, diz-se que ele tem aceleração.
Se a velocidade é constante (isto é, não varia
com o tempo), a sua aceleração é nula.
Formalmente, isto é, matematicamente, definimos a aceleração
escalar média de uma partícula como o quociente
entre a variação de velocidade e o intervalo de tempo:
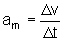
onde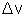 
é a diferença de velocidades da partícula
nos instantes t2 e t1, isto é,
|
|
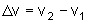
De maior importância
do que a aceleração média é a aceleração
instantânea. Como o nome indica, o interesse é
a obtenção da aceleração num determinado
instante de tempo. A maneira de defini-la, a partir da aceleração
média, é tomarmos intervalos de tempo cada vez menores,
isto é, tomarmos o limite em que o intervalo se aproxima de
zero. Esta é a situação na qual t2
é muito próximo de t1. Referimos,
portanto, à aceleração escalar instantânea
através do processo limite:
.
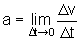A
partir da velocidade instantânea (v (t)), podemos calcular
a aceleração instantânea. Primeiramente, calculamos
a aceleração média entre os instantes t e t
+
 :
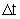e,
em seguida, fazemos
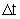= 0.
Esse
processo limite define a função derivada de v (t) (com
respeito ao tempo t) e se representa:
Gil Marques
|
|
