| |

O conceito de velocidade está intimamente ligado à variação
da posição. Se a posição de um
objeto muda com o tempo, ele está animado de velocidade. Se
ele está em repouso, sua velocidade é nula.
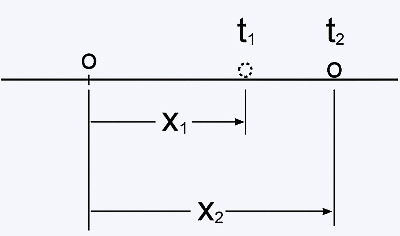
Digamos que,
no tempo t1, a partícula
estava em x1 e que,
no instante t2, ele
está em x2. Admitiremos
t2 > t1.
Assim, no intervalo
de tempos t1 dado por
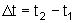 ,
,
houve uma variação da posição,
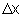 , dada por , dada por
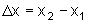 .
.
Definimos então a velocidade escalar
média como a razão entre a variação
da coordenada e o intervalo de tempo decorrido:
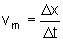 .
.
Observe-se
que a velocidade escalar média sempre faz referência
a dois instantes de tempo (por isso, falamos em média).
No entanto, a velocidade na qual temos maior interesse é a
velocidade num determinado instante de tempo. Tal velocidade é
denominada velocidade instantânea.
Para definirmos a velocidade instantânea, devemos recorrer a
um conceito matemático conhecido como limite.

Observemos que a velocidade média
é definida tomando-se dois instantes de tempo. Para defini-la
num determinado instante, basta tomarmos intervalos de tempo cada
vez menores. Dessa forma estamos assegurando que, cada vez mais, não
exista diferença entre t2 e t1. Portanto,
estaremos falando, ao tomarmos o limite no qual
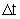 tende a zero, de um só instante de tempo.
tende a zero, de um só instante de tempo.
Definimos, portanto, a velocidade instantânea no instante t1
através do processo limite:
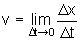 . .
O processo limite definido acima tem o nome de derivada
da função x(t) com respeito ao tempo e se representa:
Gil
Marques
|
|