Para especificarmos a posição do besouro no fio, adotamos um ponto como referência. Chamamos esse ponto simplesmente de origem O (origem do sistema de coordenadas). A partir desse ponto de origem, especificamos a coordenada do objeto da seguinte forma: primeiramente, determinamos a distância do objeto até a origem. A coordenada será o valor dessa distância se o objeto estiver à direita da origem, ou será o valor dela precedido pelo sinal menos se ele estiver à esquerda. Claramente, isso é uma convenção. Se adotarmos outra, devemos especificá-la. Para especificar a convenção que adotamos, fazemos uso de uma flecha. O sentido da flecha apenas indica o sentido no qual a coordenada terá um valor positivo. As coordenadas terão valores negativos quando a posição estiver na direção oposta à da flecha a partir da origem.

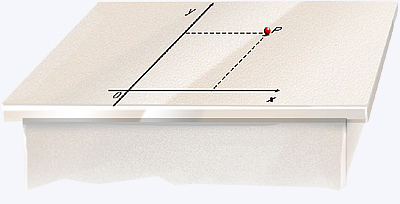
A extensão para o caso de duas dimensões pode ser entendida a partir do movimento de uma bola sobre uma mesa. As duas coordenadas (x e y) da posição P da bola seriam determinadas da seguinte forma:

Primeiramente, adota-se uma origem (O) do sistema de coordenadas. Em seguida, faz-se passar pela origem dois eixos ortogonais (isto é, retas perpendiculares) e para cada um dos eixos damos uma orientação.

Agora traçamos, a partir de P, duas retas paralelas aos eixos e tracejadas, até elas encontrarem os eixos Ox e Oy, respectivamente. Estes pontos de encontro das retas tracejadas com os eixos definem as coordenadas da posição do corpo.

No caso do movimento no espaço tridimensional, é suficiente acrescentarmos mais um eixo (z) (fig. 5). Primeiramente, traçamos uma reta paralela ao eixo z até encontrar o plano xy em P'. Para a coordenada z, adota-se o mesmo procedimento do caso unidimensional ao longo dessa reta paralela z. Para as demais coordenadas, adota-se o ponto onde a reta intercepta o plano xy.
Podemos, então, concluir que, utilizando um sistema de coordenadas cartesianas, a posição P de um objeto pode ser inteiramente especificada através do conjunto de coordenadas x, y, z:

P = (x, y, z)

Gil Marques