| |
A partir das definições anteriores, podemos verificar
as propriedades gerais que se seguem. Se
 ,
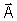e
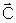são vetores, valem as propriedades de comutatividade e associatividade,
,
.
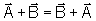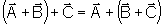Valem também as seguintes propriedades distributivas no caso
da multiplicação por escalares c e d:
,
.
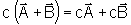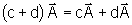Para o produto escalar de dois vetores valem as propriedades:
,
,
.
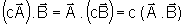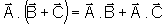Para
o produto vetorial valem
,
,
,
.
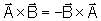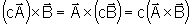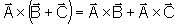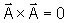Para
os versores
 ,
 ,
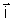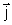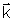valem as regras
,
,
.
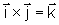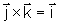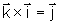As seguintes identidades são
muito úteis
,
.
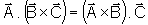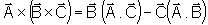Finalmente, lembramos que se definirmos o símbolo totalmente
anti-simétrico de Levi-Civita,
 ,
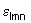como sendo dado por
=
|
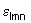0, se
quaisquer dois dos índices são iguais,
+1,
se (lmn) é uma permutação par de (123),
-1, se (lmn) é uma permutação ímpar (123), |
então,
as componentes do produto vetorial
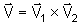
podem
ser escritas na forma
onde
está implícita a soma sobre os índices repetidos.
Gil
Marques
|
|
