| |

Como fizemos para o vetor posição podemos agora representar
qualquer vetor em coordenadas cartesianas a partir das suas componentes
x, y e z. Um vetor genérico qualquer
 será escrito como será escrito como
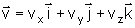
.
Tendo em vista as propriedades de ortogonalidade dos versores
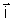 , ,
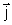 , ,
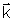 vemos que as componentes de qualquer vetor são dadas pelos
produtos escalares
vemos que as componentes de qualquer vetor são dadas pelos
produtos escalares
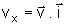 ,
,
 ,
,
 .
.
Ainda utilizando os versores
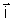 , ,
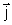 e
e
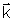 ,
podemos definir o produto vetorial de dois vetores,
formalmente, como o determinante da matriz constituída pelos
versores e pelas componentes dos vetores. Isto é, ,
podemos definir o produto vetorial de dois vetores,
formalmente, como o determinante da matriz constituída pelos
versores e pelas componentes dos vetores. Isto é,

.
Portanto,
as componentes do vetor
 são: são:


Gil Marques
|
|