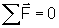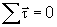Quando levantamos um peso com a mão espalmada para cima, como mostra a figura, utilizamos o bíceps. Os ossos do antebraço e braço, úmero, rádio e ulna (ou cúbito), são os diretamente utilizados nesse movimento. Através das relações básicas do equilíbrio e podemos obter a equação necessária para calcular a força do bíceps. Na figura ao lado estão mostradas esquematicamente as forças que atuam no braço. 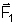é a força exercida pelo úmero na junta do cotovelo, 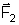é a exercida pelo bíceps no rádio e a 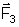é a força peso do conjunto braço e mão. 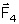é o peso que está sendo levantado. A força 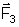está aplicada no centro de massa do conjunto braço e mão, que fica aproximadamente na metade do braço (metade da distância entre o cotovelo e o pulso, para dar conta da região mais gorda do braço). 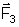pode ser estimada em 6% do peso total do indivíduo.

Os torques podem ser calculados medindo-se distâncias entre o centro do cotovelo (eixo em torno do qual o braço gira) e o ponto de aplicação de cada força. Notem a perpendicularidade entre os braços dos momentos e as forças correspondentes 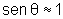. Os braços dos momentos estão indicados por r₁, r₂ é a distância entre o eixo de rotação e o ponto de inserção do bíceps no rádio (aproximadamente 3cm); r₃ é a distância entre o eixo e o centro de massa do conjunto braço e mão, e r₄ é a distância entre o eixo e o centro do objeto sustentado. Note que r₁ = 0, já que o úmero se encaixa praticamente no centro de rotação do cotovelo.

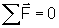
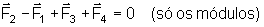
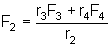
Podemos assim obter a força do bíceps nessa situação. Cuidado, quando a palma da mão estiver voltada para o outro lado, utilizamos outro conjunto de músculos.

A força do bíceps pode também ser medida com o auxílio de um dinamômetro fixo numa parede, como mostra a figura abaixo. Neste caso, note que o antebraço está apoiado sobre a mesa, de modo que 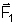não entra no problema. Também 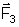, peso do braço, tem agora a mesma direção que .

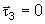Assim, considerando os módulos,

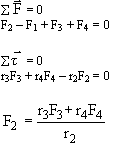
se resume a:

.

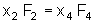Medindo-se x₄ e F₄, sabendo que x₂ = 3cm, podemos obter F₄.

	Observação:
	Estas relações de torques foram obtidas para o caso particular em que os braços dos momentos são perpendiculares às respectivas forças. Notem que sen 75º = 0,966 = 0,97. Se aproximarmos 0,97 para 1,00 estaremos cometendo um erro de 3% apenas. Já que vamos usar a distância x2 = 3cm para qualquer pessoa, esta aproximação é muito mais grosseira do que a do ângulo de 75º. Assim sendo, mesmo que o braço esteja inclinado de 75º a 105º, estaremos errando relativamente pouco. Use um transferidor para ver que até podemos inclinar bastante!

Marques e Ueta