| |
O
outro movimento do corpo rígido é o movimento
de rotação, que se observa sempre que um torque é a ele aplicado,
como num pião.
Relembrando alguns corpos em movimento de rotação, atentem para os
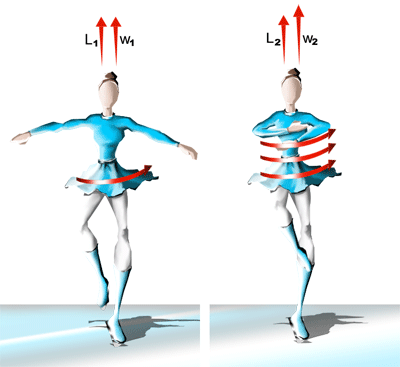
detalhes destacados no seguinte exemplo. Em espetáculos de patinação
artística no gelo, freqüentemente se vê uma patinadora girar em torno
de si mesma com os braços abertos na horizontal. Ao encolher os braços
sobre o peito, nota-se que a sua velocidade angular aumenta consideravelmente.
A distribuição de massa do corpo no espaço afeta a rotação.
No movimento de translação, quando a mesma força é aplicada a objetos
de massas diferentes, observam-se acelerações diferentes.
No movimento de rotação, quando o mesmo torque é aplicado em
objetos idênticos com distribuição diferente de massa, observam-se
acelerações angulares diferentes. Não é a massa que afeta a
velocidade angular da patinadora, mas a distribuição da massa do seu
corpo. Essa distribuição pode ser expressa através de uma quantidade
denominada momento de inércia.
O
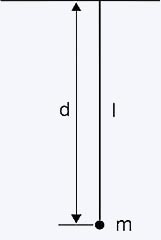
momento de inércia I de um corpo é definido em relação a um eixo de
rotação. Suponhamos, por exemplo, uma bola de massa m presa a um fio
de comprimento d. Uma pessoa gira o fio e faz a bola rodar em torno
de um ponto O. O momento de inércia da bola, em relação a um eixo
vertical que passa por O, é dado por
 .
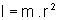Se
for um corpo extenso, é necessário subdividi-lo em pequenas porções
de massas
 ,
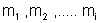cujas distâncias ao eixo de rotações são respectivamente
 .
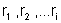O momento de inércia do corpo subdividido em n partes, em relação
ao eixo de rotação, é dado por
ou seja,
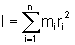
O
símbolo
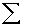é denominado somatória e é utilizado para indicar a soma de vários
termos, todos com a mesma forma. Cada termo corresponde a um valor
diferente do índice i, que pode variar de 1 a n.
Recordando, então, nas translações, as forças provocam uma aceleração,
enquanto nas rotações os torques provocam aceleração angular. Nas
translações, a massa do objeto é um parâmetro importante e, nas rotações,
é o momento de inércia que é o parâmetro correspondente.
E
a quantidade de movimento corresponde a que parâmetro na rotação?
Em gaiolas para criar preás e ratinhos, existe um tambor girante que
começa a rodar assim que o bichinho começa a andar dentro dele. Se
o animal andar em sentido anti-horário, o tambor girará para o sentido
contrário, isto é, sentido horário (o dos ponteiros de um relógio).
Existe uma compensação, existe uma conservação de alguma grandeza.
Também no exemplo da patinadora, quando o momento de inércia muda,
observa-se uma variação na velocidade angular.
Define-se uma grandeza, a quantidade de movimento angular do corpo
em rotação
 ,
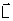que é vetorial e é dada por
 ,
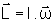onde I é o momento de inércia do corpo e
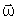é a velocidade angular. O seu módulo é dado por
 ,
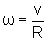como foi visto em Movimento Circular. Relembrando, v é a velocidade
tangencial e R é o raio da trajetória. A grandeza
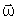é um vetor, a sua direção e sentido são definidos.
Note que, nos exemplos acima citados, observamos o movimento do rato
numa direção e o tambor na outra.
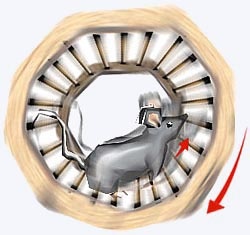
Legenda:
e
têm o mesmo módulo, a mesma direção e sentidos contrários.
No caso da patinadora, veja o desenho abaixo:
Legenda:
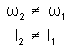
Mas
 ,
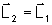já que não houve um torque adicional para alterar o movimento da bailarina.
L é a quantidade que se conserva.
O momento angular ou quantidade de movimento angular
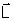corresponde, na rotação, à grandeza
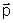na translação.
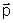de um móvel não muda se não aplicarmos uma força. Na rotação
,
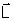não muda se não aplicarmos um torque.
Pode-se mostrar que o momento angular ou quantidade de movimento angular
está relacionado ao torque por
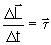
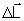é a variação da quantidade de movimento angular.
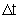é o intervalo de tempo em que o torque é aplicado.
Existem outros paralelos entre translação e rotação:
Se m é constante (não há nem perda nem ganho de massa),
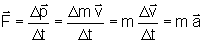
que é a 2ª lei de Newton da translação.
Se
I é constante,
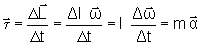
onde
é
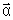aceleração angular.
Tente
lembrar agora qual a sensação vivenciada quando você passa uma enceradeira
de apenas uma escova ou, então, ao furar algum objeto com uma furadeira
elétrica. Sente-se claramente uma reação à rotação. Vocês se lembram
da ação e reação de uma força. Na rotação também existe o mesmo efeito.
Resumindo,
é possível fazer um paralelo entre translação e rotação e enunciar
leis análogas às Leis de Newton da translação.
Primeira
lei: A rotação de um corpo é mantida na ausência de torques.
Segunda lei: A variação da quantidade de movimento angular
é proporcional ao torque e ao intervalo de tempo em que o torque é
exercido.
Terceira lei: A toda ação de um torque corresponde um torque
de reação, de mesma intensidade, mesma direção mas sentidos opostos.
(Também nas rotações, a ação e a reação de um torque são aplicadas
em corpos diferentes.)
Quantidades
análogas:
Marques
e Ueta
|
|
