Num sistema de n partículas, a quantidade de movimento total se conserva quando não existe nenhuma força externa aplicada em um ponto do sistema com propriedades muito especiais, chamado centro de massa.

A posição do centro de massa é dada pela relação:

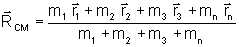
onde é a posição da i-ésima partícula e m_i, a sua massa.

Sendo M a massa total, isto é, a soma das massas, então, podemos reescrever essa equação assim:

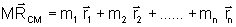
Como as massas são constantes, para se obter as razões em função do tempo em ambos os membros, num intervalo de tempo 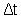tendendo a zero, basta calcular as razões em função do tempo das posições. Por outro lado, já sabemos que 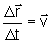, quando 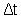tende a zero.

Da mesma forma que anteriormente, calculando-se as razões em função do tempo de ambos os membros dessa equação obteremos que, para o centro de massa do sistema de partículas, vale a lei de Newton:

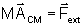
onde é a aceleração do centro de massa.

Logo, o centro de massa tem uma propriedade muito peculiar. O centro de massa se movimenta como se todas as forças externas estivessem aplicadas sobre ele.

Marques e Ueta