

| Objetivos: |
- Observar
e diferenciar atrito estático e cinético.
- Medir
a dependência da força de atrito estático
em função do peso do bloco
usado.
- Calibrar
um dinamômetro para medir forças.
- Determinar
os coeficientes de atrito estático e cinético
de diferentes blocos.
|
| Material: |
Você
vai precisar de uma superfície lisa com aproximadamente
30cm de largura e 1m de comprimento. Pode ser uma placa de madeira
muito lisa (sem envernizar!) ou recoberta de fórmica
ou plástico liso.
Você vai precisar também de blocos de madeira ou
de outro material, com formato de paralelepípedo, como
caixas. |
Escolha
em 5 blocos iguais a superfície mais uniforme, de mesma área.
Corte um pedaço de lixa fina, um de lençol de borracha
lisa, um de feltro e um de plástico, de modo que toda a superfície
escolhida fique recoberta. No último bloco, a superfície
deve ser muito bem lixada cada vez com lixa mais fina, até
que fique bem lisa.
Cada conjunto de 5 blocos deve ter a mesma área recoberta com
os diferentes materiais. Os blocos usados na sala de aula pelos diferentes
grupos de alunos devem ter praticamente a mesma massa, para possibilitar
a comparação dos valores dos coeficientes de atrito.
Espera-se a dependência do coeficiente de atrito apenas com
o par de materiais em contato.
Prenda ganchos em uma superfície do bloco para poder acoplá-lo
ao dinamômetro, como mostra a figura.
Use uma mola de aço e experimente se a deflexão causada
pela tração dos diferentes blocos não ultrapassa
10cm e se não causa deformação irreversível
da mola. Caso isso ocorra, é necessário obter outra
mola ou reduzir o tamanho dos blocos.
No conjunto testado, os blocos de madeira têm as dimensões
aproximadas de 7cm, 4cm e 5cm, a massa é de aproximadamente
170g ± 5g. A mola foi obtida usando um arame de aço
de 0,5mm de diâmetro e o comprimento total da mola é
de 3cm. O diâmetro do enrolamento é de 2,5cm.
Escolhido o conjunto adequado de blocos e mola, faça um treinamento
para tracionar os blocos, de modo a manter uma velocidade praticamente
uniforme. Nas primeiras tentativas, o bloco depois de iniciado o movimento
chega até a parar, por causa da reação da pessoa
que traciona o conjunto.
Você já vai notar a diferença entre o atrito estático
e o cinético. Observe qual é a maior e qual é
a menor deflexão observada com os 5 blocos.
Você vai precisar de um suporte para massas e massas que serão
usadas como padrões. Foram usadas arruelas com um rasgo e um
suporte, como mostra a figura ao lado, para calibrar o dinamômetro.
Procedimento:
1.
Calibre o dinamômetro escolhido. Para isso, prenda a mola no
suporte, como mostra o desenho ao lado. Na outra extremidade da mola,
acople um suporte para colocar massas conhecidas, os padrões
de massa. Meça as massas dos padrões escolhidos. Organize
os dados da calibração numa tabela, como a que segue.
| Tabela
1 - Calibração do Dinamômetro |
| |
peso
(N) |
indicação
(x) (cm) |
Deslocamento
(x-x0) (cm) |
Observação:
a)
A escolha das massas deve considerar a menor e a maior deformação
da mola observadas anteriormente.
b) x0 é a posição
de equilíbrio da mola, sem nenhuma massa acoplada.
2.
Faça o gráfico de calibração.
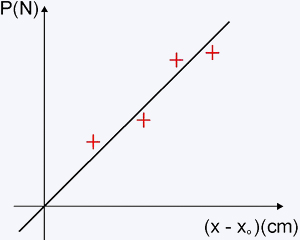
A
reta deve passar pelo zero, pela forma como as deflexões são
medidas.
3.
Acople o dinamômetro nos diferentes blocos, tracione-os sobre
a superfície lisa. para cada bloco, anote as deflexões
(x - x0)e
e da mola no momento em que o bloco começa a se movimentar
e também as deflexões (x - x0)c
quando se mantém o bloco em movimento de forma uniforme. Repita
as medições várias vezes e agrupe adequadamente
os dados. Organize os dados em uma tabela.
| Tabela
2 - Deslocamentos medidos |
| madeira
lisa |
Feltro |
plástico |
lixa |
borracha |
| (x
- x0)e
(cm) |
(x
- x0)c
(cm) |
|
| (x
- x0)e
(cm) |
(x
- x0)c
(cm) |
|
| (x
- x0)e
(cm) |
(x
- x0)c
(cm) |
|
| (x
- x0)e
(cm) |
(x
- x0)c
(cm) |
|
| (x
- x0)e
(cm) |
(x
- x0)c
(cm) |
|
| Média |
|
|
|
|
| Desvio |
|
|
|
|
4.
Utilize apenas os valores médios dos deslocamentos e, através
do gráfico de calibração, obtenha os valores
das forças aplicadas Fe e Fc, correspondentes aos atritos estático
e cinético, respectivamente.
| Tabela
3 - Coeficientes de atrito |
| Tipo
de bloco |
| massa |
peso |
Fe |
|
| (g) |
(N) |
(N) |
|
|
|
| Madeira
Feltro
Plástico |
|
|
| Etc. |
|
|
5.
Utilize os desvios dos deslocamentos e atribua o desvio experimental
correspondente para as forças obtidas através da calibração.
Atenção: Os desvios são obtidos grosseiramente
com apenas 1 significativo, então, quando você já
tiver calculado dois ou três casos, pode até avaliar
para os outros casos. Não trabalhe demais sem necessidade!
6.
Lembre-se que, ao utilizar os deslocamentos médios, determinamos
os valores médios das forças de atrito correspondentes
e do coeficiente de atrito estático e cinético. O desvio
experimental dos coeficientes deve ser obtido calculando-se os valores
máximos e mínimos de cada quociente utilizado.
7.
Compare os valores dos coeficientes obtidos por outros grupos para
cada tipo de bloco. Organize-se como sugerido abaixo:
| Tabela
4 - Resultados finais: Madeira lisa |
| |
|
|
Área |
8.
Analise a tabela final obtida e discuta.

Procedimento:
1.
Utilizando vários blocos lisos idênticos ao do experimento
anterior e o dinamômetro calibrado, medir as deflexões
causadas pela superposição de vários blocos,
sucessivamente. Organize a tabela sugerida abaixo.
| Tabela
de dados |
| Nº
de blocos |
(x-x0)e |
Fe |
N
= mg |
1 bloco
2 blocos
.............
.............
.............
|
|
|
|
2.
Faça um gráfico entre F e as normais correspondentes
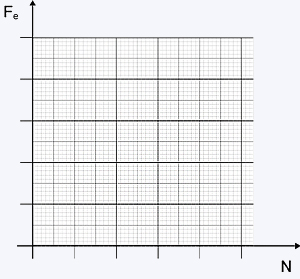
3.
Trace a reta média pelos pontos experimentais.
O coeficiente angular da reta é o coeficiente de atrito estático.
Calcule o coeficiente angular.
4.
Usando os mesmos dados do item 2, cada aluno deve traçar a
reta escolhida individualmente. Diferente alunos vão obter
retas e, portanto, coeficientes angulares diferentes. Para cada conjunto
de dados, o coeficiente angular médio é o que melhor
representa os dados e o desvio é obtido pelo (valor máximo
- valor mínimo)/2.
Atenção: A reta passa pelo zero.

1.
Use um bloco de cada vez sobre a superfície lisa. Incline a
superfície, aumentando gradativamente o ângulo
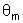 ,
conforme a figura. O ângulo
,
conforme a figura. O ângulo  a partir do qual o bloco desliza livremente é tal que
a partir do qual o bloco desliza livremente é tal que
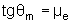 .
.
2.
Meça os valores de a e b com uma régua. Repita o procedimento
do item anterior para obter valores médios de a e de b e os
respectivos desvios.
3.
Determine o valor do coeficiente de atrito, calculando o quociente
a/b com os valores médios e o desvio do coeficiente.
4.
Use os outros blocos com diferentes superfícies. Determine
os valores correspondentes de 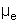 .
.
5.
Compare com os valores obtidos por outros grupos ou com os obtidos
por outros métodos.
Marques e Ueta