Um
passageiro se move num trem, o qual está em movimento em relação
a um observador em repouso (na superfície terrestre). Esse
é um exemplo típico de movimento composto. Nesse caso,
o movimento do passageiro é composto por dois movimentos: o
do passageiro em relação ao trem e do trem em relação
ao solo.
O estudo da composição de movimentos é facilitado
pelo uso da noção de vetores e as operações
de adição e subtração de grandezas vetoriais.
Para entendermos de uma forma bastante geral esse problema, consideremos
dois sistemas de referência. Vamos designá-los por e
.
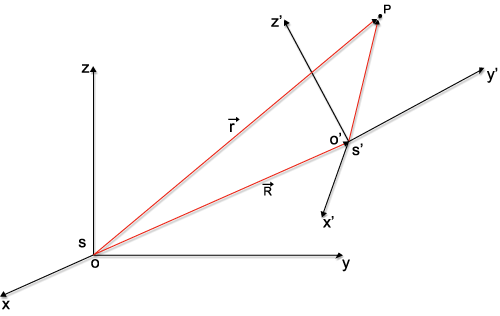
| À
origem do sistema de coordenadas (O') está associado
o vetor de posição.
A posição do ponto P é determinada, no
sistema S', pelo vetor e no sistema S, pelo vetor.
|
|
Note-se que
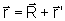
Não
é difícil concluir que a velocidade da partícula
no sistema S (designada aqui por 
0) é dada pela adição
da velocidade da partícula no sistema S' (designada 
') com a
velocidade com que o sistema S' se move em relação a
S (designada por ).
Isto é,
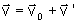
Para
a aceleração nos dois sistemas, podemos escrever:
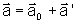
onde
a0 é a aceleração
do sistema S' em relação a S, e a e a' são as
acelerações nos sistemas S e S', respectivamente.
Marques e Ueta
