Como a aceleração da gravidade aponta na direção perpendicular à superfície terrestre, o sistema de coordenadas cartesianas mais indicado é aquele no qual um dos eixos é paralelo ao chão (eixo x) e o outro eixo é paralelo à aceleração da gravidade.

Podemos estudar o movimento do projétil com a composição de dois movimentos. Um movimento na direção vertical (eixo y) e outro movimento na direção horizontal (eixo x).

Ao longo do eixo x, e como não existe aceleração nessa direção, o movimento é uniforme e escrevemos:

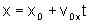
onde é a coordenada inicial (no tempo t = 0) e v_0x é a componente da velocidade inicial no eixo x.
A componente da velocidade no eixo x é constante e dada por

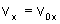
Ao passo que, ao longo do eixo y, a aceleração é constante, e dada pela aceleração da gravidade g. O movimento, no eixo y, é, portanto, uniformemente variado e, para a orientação de eixos considerada, escrevemos:

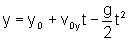
A componente da velocidade se escreve:

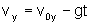
onde y₀ é coordenada inicial (eixo y) e v_0y é a componente da velocidade inicial.

A conclusão à qual chegamos é a de que, dadas a posição inicial (x₀, y₀) e a velocidade inicial (v_0x, v_0y) do projétil, podemos determinar a sua posição e velocidade em qualquer instante (t) depois do lançamento.

Para a posição, basta determinarmos x e y. Essas coordenadas são dadas, para um tempo qualquer, pelas expressões

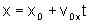
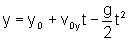
Ao passo que, para a velocidade, a qualquer t, temos a seguinte expressão para suas componentes:

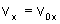
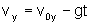
Estas são as equações básicas do movimento. Podemos, a partir delas, obter algumas informações sobre esse movimento.

Marques e Ueta