Além da representação geométrica (ou gráfica) utilizada anteriormente, podemos fazer uso de uma outra representação, conhecida como representação analítica do vetor.

Na representação analítica também utilizamos um conjunto de três atributos de um vetor (esses atributos são conhecidos como componentes do vetor). Para a definição de componentes, a melhor alternativa - e a mais fácil - é usar um conjunto de coordenadas cartesianas.

 

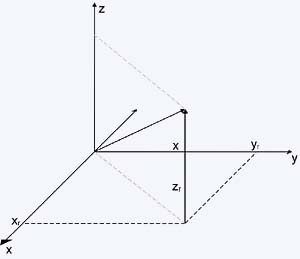
Dado um sistema de coordenadas cartesianas (composto de um conjunto de três eixos ortogonais), podemos definir as componentes de um vetor nesse sistema de eixos tomando-se as projeções do vetor nesses eixos.

Vamos tomar, por uma questão de simplicidade, um sistema com dois eixos ortogonais (x e y). Esses dois eixos estão contidos num plano.

Consideremos um vetor v nesse plano. A componente x do vetor v (designada por 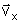) é dada pela projeção do vetor v no eixo x. Para determinarmos a projeção do vetor ao longo de qualquer eixo, consideramos as extremidades do vetor e por elas traçamos linhas perpendiculares ao eixo até encontrá-lo. Agora tomamos essa distância como a projeção se a flecha estiver na mesma direção do eixo. Caso contrário, a projeção será essa distância, mas com sinal negativo. A projeção, portanto, tem que levar em conta a orientação do vetor em relação ao eixo. A projeção fica melhor definida, matematicamente, em termos do ângulo (entre o vetor v e o eixo x). Podemos escrever:

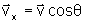
onde v é o módulo do vetor.

Analogamente, a componente y é a projeção do vetor v ao longo do eixo y. A expressão para 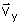é, em termos de ,

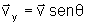
Marques e Ueta