|

No
capítulo ( ) estudamos a rotação em torno de
um eixo (eixo z). Nesse caso o ângulo de rotação
foi por nós designado por 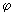 . .
Consideremos agora o caso geral de dois sistemas dos quais um experimentou
uma rotação, a mais geral possível. Imaginemos
esses sistemas ilustrados pela figura ao lado.
(FIGURA)
Podemos fazer os dois sistemas coincidirem através de 3 (três)
rotações sucessivas. Cada rotação será
caracterizada por um ângulo diferente. As rotações
aqui apresentadas levam-nos a definir os ângulos de Euler 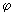 , ,
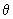 e
e 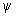 .
O ângulo .
O ângulo 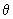 corresponde ao ângulo entre z e z', onde
corresponde ao ângulo entre z e z', onde
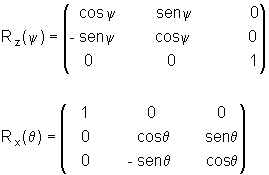
Observemos
que
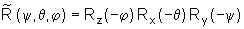
Portanto,
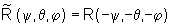
e
que
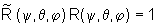
e
portanto
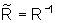
Note-se que o plano x' y' perfura o plano x y determinando um segmento
de reta (linha nodal). Os ângulos 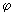 e
e 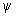 são definidos como o ângulo entre os eixos e y e x com
essa reta (linha nodal).
são definidos como o ângulo entre os eixos e y e x com
essa reta (linha nodal).
(FIGURA)
Podemos fazer os três eixos coincidirem fazendo uma rotação
em torno do eixo z do ângulo 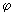 ,
em seguida uma rotação do ângulo ,
em seguida uma rotação do ângulo 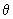 em torno da linha nodal e finalmente uma rotação de
um ângulo
em torno da linha nodal e finalmente uma rotação de
um ângulo 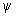 em torno do eixo z'.
em torno do eixo z'.
A relação entre as coordenadas 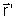 e
e 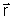 de um ponto que experimenta a rotação é
de um ponto que experimenta a rotação é
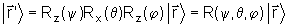
onde,
de acordo com nossa notação

|