|
Consideremos
um oscilador harmônico simples sujeito à ação
de uma força não periódica F(t).
A equação que descreve o movimento do oscilador é
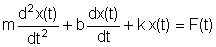
A solução da equação acima é uma
combinação de dois termos
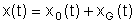
onde
x0(t) é uma solução da equação
homogênea ( ).
Para determinarmos xG(t) utilizaremos o método de
Green. Para isso procuraremos a solução da equação
( ) para um pulso de duração muito curta. Tal pulso
é representada pela função
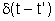
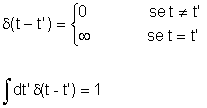
A função de Green G(t,t') é a solução
da equação para o pulso
,
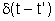isto é
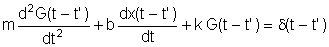
Tomando a transformada de Fourier da equação acima e
lembrando que
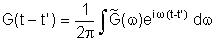
e
que
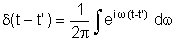
obtemos
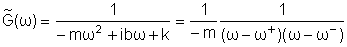
ond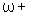e
e
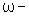são definidos em ( )
Portanto, efetuando-se a integração no plano complexo,
obtemos a partir de ( ) e ( ) que
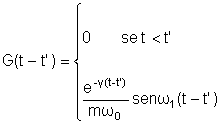
onde
em ( ) é dada por
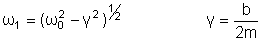
A solução geral da equação ( ) pode ser
escrita, em termos da função de Green G(t-t') como
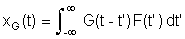
Portanto, a solução de ( ) é dada por
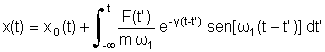
onde
x0(t) é aquela dada pela expressão ( ).
Se definirmos as matrizes e pelos seus elementos de matriz
então,
definindo os vetores
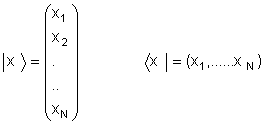
As equações de movimento que seguem de podem ser escritas
como
|
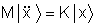
