|
Consideremos o caso em que um oscilador harmônico simples está
sujeita à ação de uma força periódica
cujo período é T. Isto é,
Falta a fórmula
Qualquer força periódica, como esta acima pode ser escrita
como uma série de Fourier:
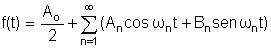
onde
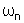é tal que
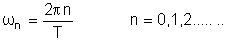
e
os coeficientes An e Bn são
tais que
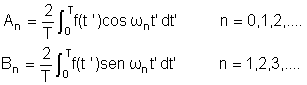
A equação para o oscilador agora é
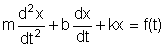
A partir de ( ) podemos verificar que a força f(t) se
decompõe na forma
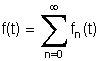
onde
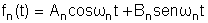
Podemos pois, escrever a solução como uma série
de Fourier
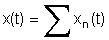
onde
cada satisfaz
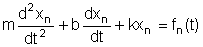
É
fácil verificar que para x(t) e F(t) dados por
( ) então x(t) dado por ( ) satisfaz ( ).
Note-se que
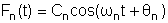
com
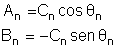
Já sabemos que a solução particular de ( ) é
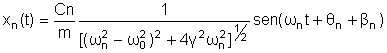
onde
Assim, a solução geral para o caso de uma força
periódica é a série de Fourier
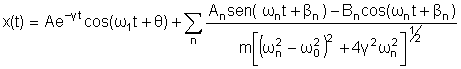
onde
os coeficientes e são dados pelas expressões ( ) e (
).
|
