Vamos analisar uma partícula cuja energia seja ligeiramente maior do que E₀ na figura. Note-se que a curva associada a E = E₁ cruza o gráfico do potencial em dois pontos associados a x₁ e x₂.

Esses pontos x₁ e x₂, como visto anteriormente, são os pontos de retorno. O movimento da partícula se confirmará aos pontos tais que

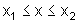
Vamos agora analisar os possíveis movimentos quando a partícula inicialmente em é deslocada ligeiramente da sua posição de equilíbrio.

Expandindo-se o potencial numa série de Taylor em torno de obteremos

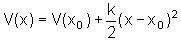
onde

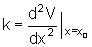
Portanto

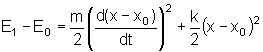
donde podemos afirmar que a partícula executará um movimento harmônico simples em torno de com período dado pela expressão ( ).

Se fizermos a mesma expansão em torno de x₃ nos dará

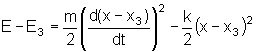
onde

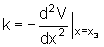
conclui-se de que a solução será

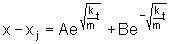
Portanto, à medida que o tempo passa a partícula se afasta de x₃. Ela não retorna ao ponto de equilíbrio. Procura se afastar o mais que ela puder. O equilíbrio em x₃ é portanto instável.