|
Consideremos
o movimento de uma partícula sujeito a dois vínculos
(duas superfícies)
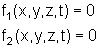
As reações normais às superfícies 1 e
2 serão dadas por
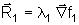
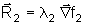
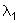e
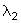são conhecidos como multiplicadores de Lagrange já que
as reações normais são ortogonais às superfícies
e que ( )
e ( )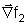
são perpendiculares às superfícies.
Portanto, podemos incorporar os vínculos holonomicos ao formalismo
Lagrangiano acrescentando à Lagrangiana os dois multiplicadores
de Lagrang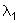e
e
.
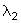Escrevemos, pois, para o sistema com vínculos
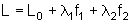
onde
L0 é a Lagrangiana sem levar em conta o vínculo.
E portanto, as novas equações de movimento serão:
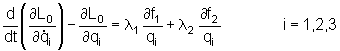
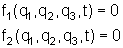
Temos, portanto, um conjunto de 5 equações e 5 incógnitas
 .
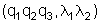Esse é o método dos multiplicadores de Lagrange.
A determinação de
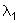e
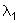nos permite agora determinar as reações normais à
superfície.
|
