|
Um
tensor de 9 componentes tem a forma geral:
 .
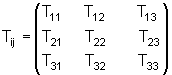Pode-se escolher, mediante uma rotação, um sistema de
eixos tais que, nesses novos eixos, a matriz T simétrica tem
a forma diagonal. Isto é,
 .
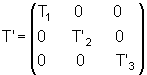Os valores T'11, T'22
e T'33 são denominados autovalores
de ou ainda valores característicos de T.
Os novos eixos x, y e z são tais
.
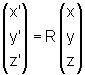Esses novos eixos são ortogonais entre si, isto é
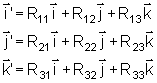
são
tais que
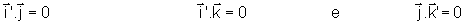
uma
vez que
 .
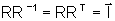Estes
novos eixos são conhecidos como eixos principais.
Qualquer vetor
paralelo aos eixos principais é um autovetor de T e para ele
vale
.
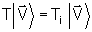Essa equação é conhecida como equação
de autovalores e ela se escreve
.
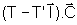Em termos das componentes podemos escrever
.
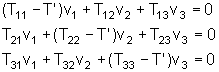Teremos soluções diferentes da trivial (v1
= v2 = v3=0)
sob e somente se o determinante associado a essa linear homogênea
for nulo, isto é:
.
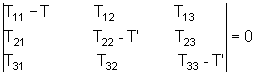A equação acima exibe três soluções
independentes (pode haver casos de soluções degeneradas
as quais serão tratadas posteriormente). Estas raízes
T'1, T'2
e T'3 são os autovalores procurados.
Isto é, são os valores de T na forma diagonal.
Para cada valor de T'(T'1, T'2
e T'3) obteremos os vetores
,
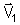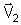e
 .
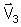Os vetores
,
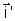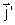e
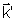são dados por
 .
|
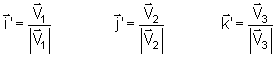