Uma vez definida a matriz de rotação R(, , 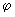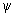) podemos definir vetores, de uma maneira geral, e tensores.
Um vetor é um ente físico definido por três quantidades v₁, v₂, v₃ de tal forma que sob uma rotação ele se transforma da mesma forma que as coordenadas. Isto é,

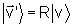
onde

ou seja, cada coordenada se transforma como

.

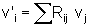Podemos definir agora um tensor como um objeto de 9 componentes, T₁₁...T₃₃, de tal forma que sob uma rotação ele se transforma

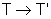
onde

.

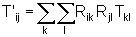Mais geralmente, definimos um tensor de posto S como um objeto 3_Sde componente tal que essas componentes se transformam como

.

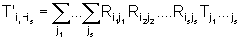Podemos escrever essa transformação sob a forma

.

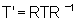Transformações como essa são denominadas transformações de semelhança.
Um tensor é dito simétrico se

T_ij = T_ji

e anti-simétrico se

T_ij = - T_ji .

O termo de um tensor é dado pela soma dos elementos da diagonal da matriz 3 x 3. Isto é

.

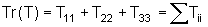O determinante de T é o determinante da matriz, isto é

.
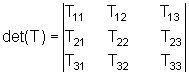