|

Suponhamos o quadro ABCD plano, girando com movimento de rotação
uniforme de velocidade
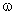 em um campo magnético uniforme de indução magnética
em um campo magnético uniforme de indução magnética
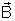 . Sabemos que, numa posição do quadro na qual a sua normal
faz com o campo um ângulo
. Sabemos que, numa posição do quadro na qual a sua normal
faz com o campo um ângulo
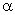 , o fluxo que atravessa o quadro vale:
, o fluxo que atravessa o quadro vale:
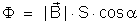
À
medida que o quadro gira, varia o ângulo
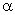 , e, portanto o fluxo
, e, portanto o fluxo
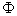 . Há, então, indução no quadro e aparece no condutor uma
corrente elétrica i (fig. 310).
. Há, então, indução no quadro e aparece no condutor uma
corrente elétrica i (fig. 310).
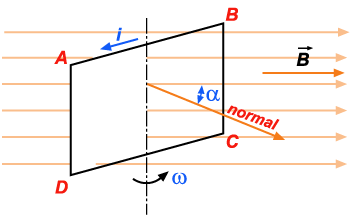
Figura 310
No
Capítulo 13 já estudamos a variação do fluxo em função do ângulo
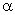 em um caso desses. Vimos que a variação do fluxo é cosenoidal,
como indica a figura abaixo. É muito importante exprimirmos
a variação do fluxo em função do tempo, à medida que o quadro gira.
Para isso, comecemos a contar o tempo de rotação do quadro no instante
em que
em um caso desses. Vimos que a variação do fluxo é cosenoidal,
como indica a figura abaixo. É muito importante exprimirmos
a variação do fluxo em função do tempo, à medida que o quadro gira.
Para isso, comecemos a contar o tempo de rotação do quadro no instante
em que
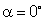 . Nesse caso, num instante t qualquer, o ângulo
. Nesse caso, num instante t qualquer, o ângulo
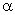 vale:
vale:
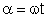 . E o fluxo, nesse instante, é expresso por :
. E o fluxo, nesse instante, é expresso por :

Figura 311
À
medida que o quadro gira, o fluxo varia proporcionalmente a
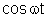 . Para fazermos uma representação gráfica do fluxo em função
do tempo basta observarmos que, chamando T ao período de rotação
do quadro, temos:
. Para fazermos uma representação gráfica do fluxo em função
do tempo basta observarmos que, chamando T ao período de rotação
do quadro, temos:

Basta
então na figura 311-a substituir os valores de
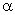 pelos valores correspondentes de t e resulta o gráfico do
segundo gráfico que exprime
pelos valores correspondentes de t e resulta o gráfico do
segundo gráfico que exprime
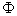 em função de t.
em função de t.

Pela
lei de Faraday-Neumann essa f.e.m. é igual à derivada do fluxo em
relação ao tempo:
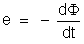
Sendo
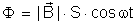 , resulta
, resulta
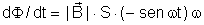 .
.
Logo,
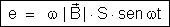
Sendo
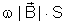 constante, essa expressão indica que e é diretamente proporcional
a
constante, essa expressão indica que e é diretamente proporcional
a
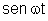 .
.

1a) Quando
um quadro plano gira com movimento de rotação uniforme dentro
de um campo magnético uniforme, a força eletromotriz induzida
no quadro é uma função senoidal do tempo. Uma força eletromotriz
desse tipo é chamada, por definição, força eletromotriz alternativa
senoidal. A representação gráfica de i em função de t está na
figura 313.
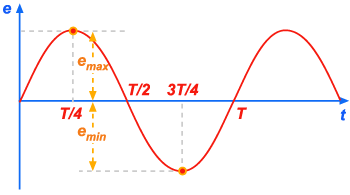
Figura 312
2a) Vemos
que a f.e.m. induzida é diretamente proporcional a velocidade
angular w do quadro. Portanto, para obtermos grande f.e.m. é
necessário que o quadro gire muito depressa. É a conclusão que
tínhamos chegado quando demos a interpretação física da lei de
Faraday-Neumann.

Seja:

Temos
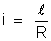
ou
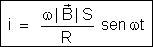
Sendo
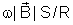 constante, essa expressão mostra que i é diretamente proporcional
a
constante, essa expressão mostra que i é diretamente proporcional
a
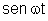 . O valor máximo da corrente é aquele para o qual
. O valor máximo da corrente é aquele para o qual
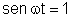 , isto é:
, isto é:

Podemos
escrever :


1a) A
corrente elétrica induzida no quadro é uma função senoidal do
tempo. Uma corrente desse tipo é chamada corrente alternativa
senoidal.
A
representação gráfica de i em função de t está indicada na figura 312.
Essa corrente é chamada alternativa, ou alternada, porque ela
percorre o condutor ora num sentido, ora noutro. A figura abaixo
indica o seguinte: que a corrente no início tem valor zero; vai
aumentando, até atingir um máximo em
 ; depois vai diminuindo até se anular em
; depois vai diminuindo até se anular em
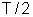 ; depois muda de sentido e vai aumentando até atingir um
máximo em
; depois muda de sentido e vai aumentando até atingir um
máximo em
 ; depois vai diminuindo, até se anular em T; muda de sentido
novamente, e reinicia o ciclo.
; depois vai diminuindo, até se anular em T; muda de sentido
novamente, e reinicia o ciclo.
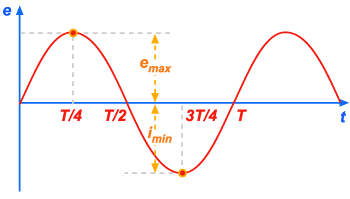
Figura 313
Vemos
que o tempo T que a corrente demora para realizar um ciclo completo
é igual ao tempo T que o quadro demora para dar uma volta no campo
magnético.
Na
corrente usada na cidade de São Paulo esse tempo T é de 1/60 segundo,
isto é, a corrente muda de sentido 60 vezes por segundo. Na corrente
usada no Rio de Janeiro, esse tempo T é de 1/50 segundo.
2a) Como
era de se esperar, vemos pela fórmula 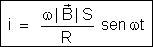 que a corrente induzida também é diretamente proporcional à velocidade
angular w do quadro. Isso está de acordo com a lei de Faraday-Neumann:
a corrente induzida será tanto maior quanto mais rápida for a
variação do fluxo.
que a corrente induzida também é diretamente proporcional à velocidade
angular w do quadro. Isso está de acordo com a lei de Faraday-Neumann:
a corrente induzida será tanto maior quanto mais rápida for a
variação do fluxo.
Recomendamos
ao leitor estudar muito bem este parágrafo, porque a indução num
quadro plano girando em campo uniforme é a mais importante aplicação
do eletromagnetismo em benefício da sociedade, pois neles se baseiam
os geradores de corrente elétrica de alta energia, como por exemplo,
os que fornecem eletricidade às cidades.
|