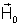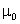Imaginemos um campo magnético  produzido no vácuo.  Para maior facilidade, suponhamos que esse campo seja uniforme.  Representemos por  a permeabilidade magnética do vácuo e por 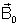 a indução num ponto qualquer desse campo.  Temos então, para qualquer ponto desse campo, a relação: .

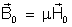Suponhamos agora que nesse campo seja colocada uma barra de uma substância magnética, por exemplo, de ferro.  Essa barra se tornará um ímã SN (fig. 256).  Calculemos a indução magnética 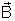 em um ponto qualquer A desse ímã.  Para isso calculemos a indução magnética produzida em A devida à magnetização da barra, e somemos com a indução 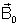 que já existia antes de a barra ser colocada no campo.

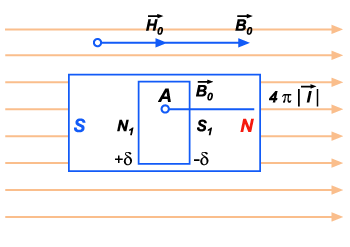
Figura 256

Na indução magnética produzida em A devida à magnetização da própria barra só influem as partes da barra infinitamente próximas do ponto A.  Imaginemos então traçada no interior do ímã uma cavidade retangular de lados infinitamente próximos, perpendicular ao campo e contendo o ponto A no seu interior (fig. 256).

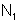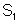Sabemos que, quando cortamos o ímã, os seus polos não ficam isolados, mas nos lugares de corte aparecem novos polos de densidades magnéticas iguais às dos polos primitivos.  Assim, na cavidade retangular aparecerão polos  e  de densidades magnéticas 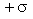 e 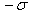 respectivamente.

O ponto A estará então entre dois polos planos, paralelos, infinitamente próximos e de densidades magnéticas 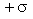 e 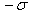.  Já vimos que nessas condições esses polos produzem em A uma indução magnética igual a 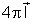, de acordo com a fórmula (153).

Então a indução no ponto será a soma de 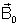 com 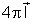, isto é, será:

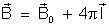
ou

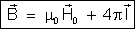
Sendo 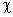 a susceptibilidade da barra imantada, sabemos que 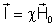.  Substituindo na fórmula anterior, ela fica:

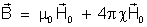
ou

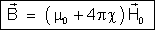
As expressões 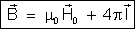e 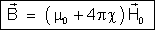dão, portanto, a indução magnética no interior de um ímã em função da susceptibilidade magnética do ímã, da permeabilidade magnética do vácuo e do campo indutor 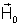 suposto no vácuo.

Suponhamos que uma barra de permeabilidade magnética 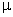 seja colocada num campo magnético de intensidade 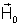, produzido no vácuo.  Essa barra adquirirá uma indução magnética B, que está ligada a 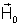 pela relação:

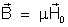
Comparando com a fórmula 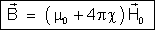temos :

 

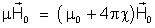
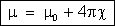
Concluímos que a permeabilidade magnética de uma substância é igual à soma da permeabilidade magnética do vácuo com 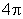 vezes a susceptibilidade magnética da substância.