|
| |
Assim
como em Eletrostática introduzimos o conceito de carga elétrica
para podermos medir a força entre corpos eletrizados, em magnetismo
introduzimos o conceito de massa magnética para que possamos medir
a força entre corpos imantados. E, analogamente ao que acontece
com carga elétrica, não temos elementos para dar uma definição de
massa magnética. Consideramo-la um conceito primitivo e fixamos
uma convenção que nos permite dizer quando duas massas magnéticas
são iguais, ou uma é múltipla da outra. Do mesmo modo que no caso
da carga elétrica, para fixarmos o critério de igualdade e multiplicidade
de duas massas magnéticas precisamos considerar massas magnéticas
ideais, chamadas massas magnéticas puntiformes. Massa magnética
puntiforme é aquela contida em uma região polar cujas dimensões
possam ser desprezadas relativamente ao problema em que está sendo
considerada; em outras palavras, a região polar fica reduzida a
um ponto (fig. 226).
Suponhamos
que desejamos comparar a massa magnética da região polar
N do ímã 1 com a massa magnética da região polar N
do ímã 2. Para isso usamos um terceiro ímã, o ímã 3 (fig. 226),
e avaliamos a força que os polos norte de 1 e 2 exercem
sobre o polo sul, por exemplo, do ímã 3. Quando o
ímã 3 é colocado próximo do ímã 1, não vai haver
ação só da região N de 1 sobre a região S de 3, mas sim,
das duas regiões de 1 sobre as duas regiões de 3. Como
nos interessa saber só a ação de N de 1 sobre S de 3, imaginamos
os dois ímãs suficientemente compridos para que possamos
desprezar os efeitos das regiões polares que não nos interessam,
que são a S de 1 e N de 3.
|
 Figura 266 |
A
região N de 1, colocada à distância d da região S de 3, em certo
ambiente dá origem à força
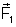. A região N de 2, colocada à mesma distância d da região
S de 3, no mesmo ambiente, dá origem à força
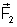. Relativamente aos módulos d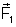e
e
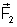há dois casos:
1o
caso:
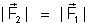
2o
caso:
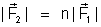
Convencionamos
que, no 1o caso, a massa magnética da região N de 1 é
igual à massa magnética da região N de 2. E que, no 2o
caso, a massa magnética da região N de 2 é igual a n vezes a massa
magnética da região N de 1. Representando por
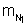e
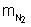respectivamente, essas massas magnéticas, temos:
no
1o caso:
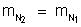
no
2o caso:
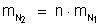
Escolhendo
arbitrariamente a massa
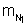como unidade, e adotando esse critério, podemos medir a
massa magnética
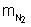. No primeiro caso, teríamos
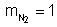; no segundo caso,
.
1a) É
importante notar que os critérios de igualdade e multiplicidade
consistem em se medirem as massas magnéticas por números proporcionais
às forças que essas massas magnéticas conseguem exercer.
Pois, sendo
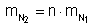ao mesmo tempo que
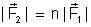, temos:
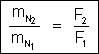
2a) A
região N de 1 exerce sobre a região S de 3 uma força
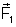de atração, à distância d. Se colocarmos à mesma
distância d a região S de 1 e a região S de 3, observaremos
entre elas uma força de repulsão de mesmo módulo que
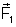. E, se as regiões polares N e S de um mesmo ímã nas
mesmas condições exercem forças iguais, concluímos que elas
tem igual massa magnética. Mas como uma exerce força de atração
quando a outra exerce força de repulsão, convencionamos considerar
positiva a massa magnética da região N e negativa a da região
S. Para um mesmo ímã, temos, então:
|
|
|
|
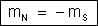
