|
| |

Há vários
processos para a medida de uma resistência. Veremos três:
1o) pela
ponte de Wheatstone;
2o) pelo método de substituição;
3o) pelo método do voltômetro e amperômetro.

Para
medirmos uma resistência
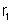 pela ponte de Wheatstone, ligamos
pela ponte de Wheatstone, ligamos
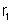 com mais três resistências conhecidas,
com mais três resistências conhecidas,
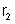 ,
,
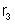 e
e
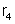 , de acordo com a figura 188. Entre
A e C ligamos um gerador, que vai fornecer corrente
ao circuito. Entre B e D ligamos um galvanômetro
G ou qualquer outro dispositivo capaz de acusar
uma diferença de potencial entre esses dois pontos.
Se o potencial de B for maior que o de D, a corrente
, de acordo com a figura 188. Entre
A e C ligamos um gerador, que vai fornecer corrente
ao circuito. Entre B e D ligamos um galvanômetro
G ou qualquer outro dispositivo capaz de acusar
uma diferença de potencial entre esses dois pontos.
Se o potencial de B for maior que o de D, a corrente
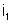 se desdobrará em duas no ponto B: uma que
percorrerá o ramo BD, outra que percorrerá BC.
Se o potencial de D for maior que o de B, a corrente
se desdobrará em duas no ponto B: uma que
percorrerá o ramo BD, outra que percorrerá BC.
Se o potencial de D for maior que o de B, a corrente
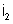 se desdobrará em duas: uma que percorrerá
DB, outra que percorrerá DC. Mas, se o potencial
de B for igual ao de D, nenhuma das duas correntes
se desdobrará:
se desdobrará em duas: uma que percorrerá
DB, outra que percorrerá DC. Mas, se o potencial
de B for igual ao de D, nenhuma das duas correntes
se desdobrará:
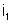 percorrerá
percorrerá
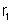 e
e
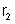 , e
, e
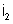 percorrerá
percorrerá
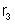 e
e
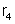 .
.
|
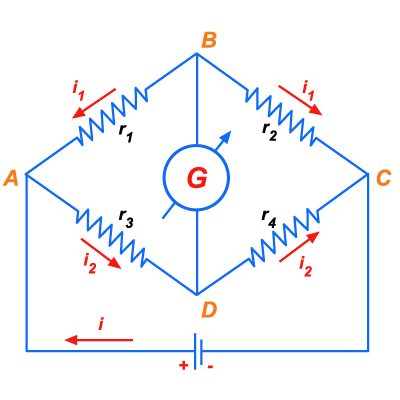
Figura 188 |
Admitamos
então que as resistências conhecidas
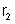 ,
,
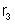 e
e
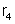 sejam escolhidas de tal modo que o potencial de
B seja igual ao de D. Nesse caso, o galvanômetro não acusa
a passagem de corrente alguma. Vejamos qual a conclusão
a que chegaremos. Temos:
sejam escolhidas de tal modo que o potencial de
B seja igual ao de D. Nesse caso, o galvanômetro não acusa
a passagem de corrente alguma. Vejamos qual a conclusão
a que chegaremos. Temos:
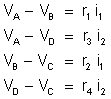
Sendo
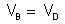 , temos:
, temos:
 e
e
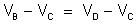
isto
é:
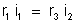 e
e
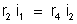
Dividindo
membro a membro essas igualdades, temos:
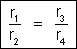 ou
ou

Concluímos
que quando os potenciais de B e D são iguais. os produtos
das resistências opostas são iguais. Tiramos:
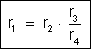

Para
medirmos a resistência
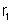 pela ponte de Wheatstone devemos ajustar os valores
de
pela ponte de Wheatstone devemos ajustar os valores
de
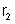 ,
,
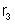 e
e
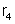 até que não passe corrente pelo galvanômetro. Então
o potencial do ponto B estará igual ao potencial do ponto
D. Nesse caso a equação
até que não passe corrente pelo galvanômetro. Então
o potencial do ponto B estará igual ao potencial do ponto
D. Nesse caso a equação
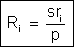 é satisfeita e calculamos por ela o valor de
é satisfeita e calculamos por ela o valor de
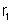 . Para tornarmos o potencial de B igual ao potencial
de D há dois processos:
. Para tornarmos o potencial de B igual ao potencial
de D há dois processos:
1o) manter
fixas as resistências
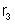 e
e
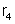 e variar
e variar
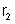 até que o galvanômetro não acuse passagem de corrente;
até que o galvanômetro não acuse passagem de corrente;
2o) manter fixa
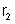 e variar o quociente
e variar o quociente
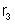 /
/
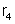 até que o galvanômetro não acuse passagem de corrente.
Este 2o processo é realizado comodamente introduzindo-se
uma simplificação na ponte de Wheatstone, com a qual a ponte
é às vezes chamada ponte de fio, ou ponte de corda.
até que o galvanômetro não acuse passagem de corrente.
Este 2o processo é realizado comodamente introduzindo-se
uma simplificação na ponte de Wheatstone, com a qual a ponte
é às vezes chamada ponte de fio, ou ponte de corda.
Ponte
de fio – Se os condutores
AD e DC forem de mesmo material e tiverem mesma secção transversal,
a relação de suas resistências é igual à relação de seus
comprimentos, isto é:
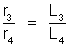
A incógnita
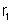 será dada por:
será dada por:
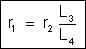
Consegue-se
isso fazendo-se com que ADC seja um fio único, e o ponto
D seja um cursor que se desloca sobre esse fio (fig. 189). O cursor
é deslocado até que não passe corrente pelo galvanômetro.
Esse fio ADC está assentado sobre uma régua graduada que
dá os comprimentos AD e DC (
 e
e
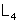 ). Em geral essa régua não é graduada para dar
). Em geral essa régua não é graduada para dar
 e
e
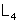 , separadamente mas, para dar o quociente
, separadamente mas, para dar o quociente
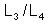 .
.
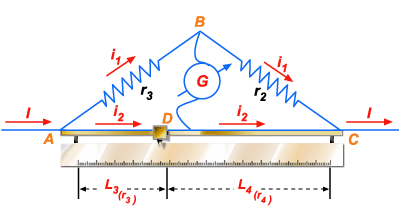
Figura 189


Forma-se
um circuito com uma pilha de f.e.m. E, um miliamperômetro
e a resistência incógnita r (fig. 190). O miliamperômetro
indicará a passagem de uma corrente i. Chamando
R à soma das resistências da pilha e do miliamperômetro,
temos pela lei de Pouillet:
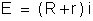
Depois
substituímos a resistência incógnita r por uma resistência
conhecida
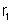 . O miliamperômetro indicará uma outra corrente,
. O miliamperômetro indicará uma outra corrente,
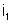 . Teremos:
. Teremos:
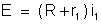
Logo,
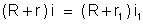
|
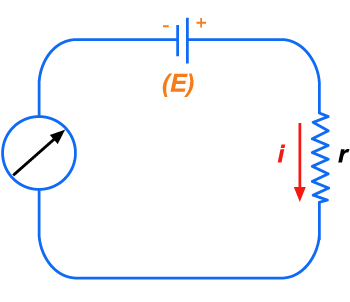 Figura 190 Figura 190 |
donde:
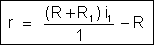
Obtemos
assim r em função de valores conhecidos
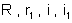 .
.

A
resistência incógnita r é ligada em série com um
miliamperômetro A de resistência conhecida
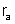 . Entre os pontos B e C é ligado um voltômetro
V. Os pontos B e C são ligados aos polos de uma
pilha, como indica a figura 191. O miliamperômetro
indica a corrente i que passa por ele e pela resistência
r. O voltômetro indica a diferença de potencial
v entre B e C. Pela lei de Ohm, temos:
. Entre os pontos B e C é ligado um voltômetro
V. Os pontos B e C são ligados aos polos de uma
pilha, como indica a figura 191. O miliamperômetro
indica a corrente i que passa por ele e pela resistência
r. O voltômetro indica a diferença de potencial
v entre B e C. Pela lei de Ohm, temos:
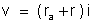
donde
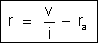
|
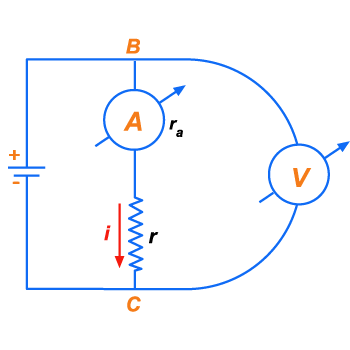 Figura 191 Figura 191 |
Ainda
com o voltômetro e amperômetro se pode medir a resistência
r montando-se o circuito como está indicado na figura 192.
O voltômetro V é ligado em paralelo com r. Deve-se conhecer
a resistência
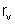 do voltômetro. Deixamos a cargo do leitor demonstrar
que, neste caso, a resistência r é dada por:
do voltômetro. Deixamos a cargo do leitor demonstrar
que, neste caso, a resistência r é dada por:
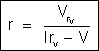
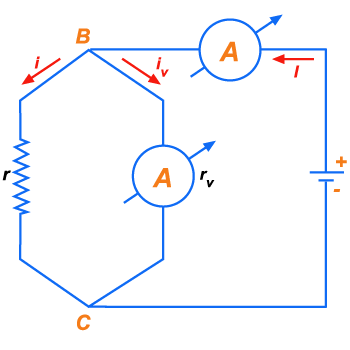
Figura 192
|
|
|