
Já vimos
que quando não há gerador nem receptor entre dois pontos A
e B, a lei de Ohm estabelece que:
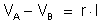
onde r
é a resistência do trecho AB. Suponhamos agora um circuito
como o que está indicado na figura 174. Acompanhando
o sentido em que a corrente circula, no trecho BA desse circuito
estão ligados em série:
1o
um gerador G de resistência interna
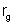 e f.e.m.
e f.e.m.
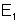 ;
;
2o um receptor R de resistência interna
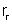 e f.c.e.m.
e f.c.e.m.
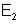 ;
;
3o uma resistência qualquer
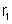 .
.
Entre
os mesmos pontos A e B é ligada uma resistência r que fecha
o circuito. Sendo I a intensidade da corrente, podemos escrever
que a diferença de potencial entre A e B vale:

Veremos
agora que essa diferença de potencial pode ser expressa de
outra maneira. Durante um tempo t o gerador fornece ao circuito
a energia
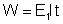 . Com essa energia fornecida acontece o seguinte:
. Com essa energia fornecida acontece o seguinte:
1o a resistência interna do gerador absorve a energia
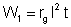 ;
;
2o
a resistência interna do receptor absorve a energia
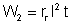 ;
;
3o a resistência
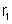 absorve a energia
absorve a energia
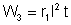 ;
;
4o de acordo com a fórmula
 o receptor absorve do circuito, para transformá-la em outro
tipo de energia, a energia
o receptor absorve do circuito, para transformá-la em outro
tipo de energia, a energia
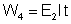 ;
;
5o a resistência r absorve a energia
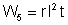 .
.
Pelo princípio
da conservação da energia, a energia fornecida pelo gerador
deve ser igual à soma das energias absorvidas:
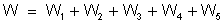
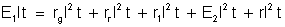
ou
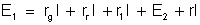
ou
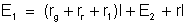
Mas, o
gerador, o receptor e a resistência
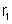 estão em série; logo as suas resistências se somam.
Fazendo
estão em série; logo as suas resistências se somam.
Fazendo
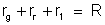
que é
então a resistência total entre B e A, temos:
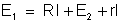
Mas,
rl é igual à diferença de potencial
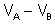 . Logo,
. Logo,
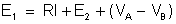
ou
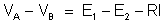

Figura 174
Observemos
que ficou agora demonstrado o que tínhamos dito no parágrafo
anterior: que quando um receptor está em série com um gerador
a força contra-eletromotriz do receptor é subtraída da força
eletromotriz do gerador. Fazendo
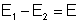 , temos:
, temos:
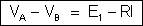
Concluímos
que “a diferença de potencial entre A e B é igual à soma algébrica
de todas as forças eletromotrizes e contra-eletromotrizes
existentes no trecho BA menos o produto da resistência total
do trecho BA pela intensidade da corrente”.
Temos
então duas fórmulas para calcular a diferença de potencial
entre A e B:

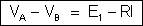 (2).
(2).