Um condutor
é representado por um dos dois modos indicados na figura 122.
Os condutores
podem ser associados de dois modos: em série, e em paralelo
(ou em derivação).
|
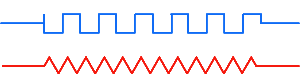 Figura 122 Figura 122 |

É aquela na
qual os condutores são ligados de maneira que o fim de cada um coincida
com o início do seguinte (fig.123).
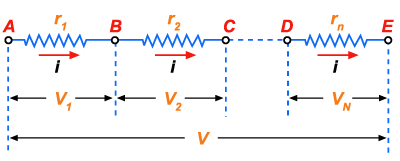
Figura 123
Sejam
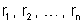 as resistências dos condutores;
as resistências dos condutores;
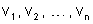 as diferenças de potencial entre seus extremos e V a diferença
de potencial entre os extremos da associação. As características
da associação em série são as seguintes:
as diferenças de potencial entre seus extremos e V a diferença
de potencial entre os extremos da associação. As características
da associação em série são as seguintes:

A intensidade
de corrente que passa por todos os condutores num dado instante
é a mesma. Não pode haver aumento nem diminuição da intensidade
ao passar do condutor AB para BC, por exemplo, por causa do princípio
da conservação da energia.

Sendo
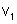 a diferença de potencial entre os extremos do primeiro
condutor e i a intensidade de corrente, a potência dissipada nesse
primeiro condutor é:
a diferença de potencial entre os extremos do primeiro
condutor e i a intensidade de corrente, a potência dissipada nesse
primeiro condutor é:
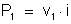
Analogamente,
a potência dissipada no segundo condutor é:
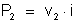
A potência
dissipada no ene-ésimo é:
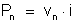
A potência
dissipada pela associação inteira é a soma das potências dissipadas
pelos condutores:
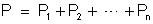
ou
Mas,
sendo V a diferença de potencial entre os extremos da associação,
podemos escrever que a potência dissipada pela associação é:
Comparando
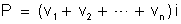 e
e
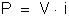 ,
temos:
,
temos:
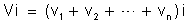
ou
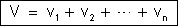

Numa
associação em série de condutores, a diferença de potencial
entre os extremos da associação é igual à soma das diferenças
de potencial entre os extremos dos condutores. |

Chama-se condutor
equivalente à associação a um condutor capaz de substituir a associação,
isto é, que suportando a diferença de potencial V que a associação
suporta é percorrido pela mesma corrente i que a associação (fig.124).
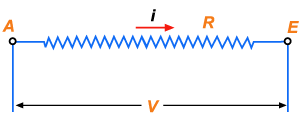
Figura 124
Sendo R a
resistência do condutor equivalente, pela lei de Ohm temos:
A
lei de Ohm, aplicada ao primeiro condutor, dá:
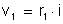
A lei de Ohm,
aplicada ao segundo condutor, dá:
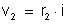
A lei de Ohm,
aplicada ao ene-ésimo condutor, dá:
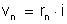
Somando-se
membro a membro:
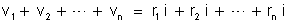
Comparando
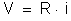 e
e
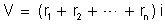 ,
resulta:
,
resulta:
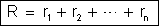

Condutores
associados em série equivalem a um condutor único cuja resistência
é igual à soma das suas resistência. |

Os condutores
tem resistências iguais, isto é,
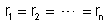 . É fácil provar que neste caso resulta também
. É fácil provar que neste caso resulta também
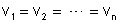 . Chamando respectivamente, r e v à resistência e à
diferença de potencial entre os extremos de cada condutor, temos:
. Chamando respectivamente, r e v à resistência e à
diferença de potencial entre os extremos de cada condutor, temos:
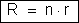
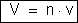


É aquela na
qual todos os condutores são ligados entre dois pontos, A e B (fig.125).
Cada condutor é chamado uma derivação.
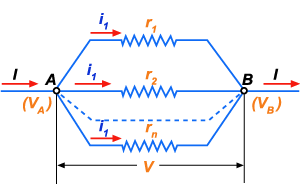
Figura 125
Sejam
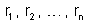 as resistências dos condutores,
as resistências dos condutores,
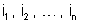 as intensidades de corrente nas derivações; I a corrente
fora da associação (corrente total);
as intensidades de corrente nas derivações; I a corrente
fora da associação (corrente total);
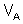 o potencial do ponto A,
o potencial do ponto A,
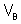 o do ponto B, de maneira que a diferença de potencial entre
A e B é
o do ponto B, de maneira que a diferença de potencial entre
A e B é
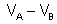 , que chamaremos simplesmente V. As características da associação
são as seguintes.
, que chamaremos simplesmente V. As características da associação
são as seguintes.

Todas as extremidades
ligadas ao ponto A tem potencial
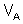 . Todas as ligadas ao ponto B tem o potencial
. Todas as ligadas ao ponto B tem o potencial
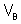 . Logo, todos os condutores suportam a mesma diferença
de potencial V.
. Logo, todos os condutores suportam a mesma diferença
de potencial V.

1a
lei de Kirchhoff – As intensidades de corrente obedecem
a uma lei chamada 1a lei de Kirchhoff, que é: “a intensidade
de corrente antes e depois da associação é a mesma e vale a soma
das intensidades nas derivações”.
A intensidade
antes e depois da associação é a mesma, porque se não fosse, haveria
ganho ou perda de corrente enquanto a corrente atravessa a associação.
Mas, ganho ou perda de corrente elétrica significa ganho ou perda
de energia. Isso é contra o princípio da conservação de energia.
Pelo mesmo motivo a intensidade fora da associação é a soma das
intensidades nas derivações, isto é:
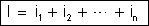

A lei de Ohm,
aplicada ao 1o condutor dá:
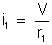
A lei de Ohm,
aplicada ao 2o condutor dá:
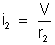
A lei de Ohm,
aplicada ao no condutor dá:
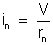
Somando membro
a membro essas expressões, temos:
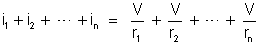
ou
Chama-se condutor
equivalente à associação a um condutor que, colocado entre os
pontos A e B permite a passagem da corrente com a mesma intensidade
I que ela tem fora da associação. Sendo R a resistência do condutor
equivalente, temos, de acordo com a sua própria definição:
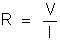 , ou
, ou
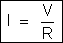 |
|
Comparando
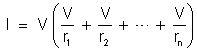 e
e
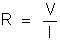 ,
temos:
,
temos:
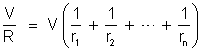
ou
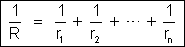
É a 2a
lei de Kirchhoff: “o inverso da resistência do condutor equivalente
é igual à soma dos inversos das resistências das derivações”.

Os condutores
tem resistências iguais, isto é,
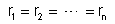 (que chamaremos r). Neste caso as intensidades de corrente
nas derivações também são iguais:
(que chamaremos r). Neste caso as intensidades de corrente
nas derivações também são iguais:
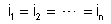 (que chamaremos i).
(que chamaremos i).
A 1a
lei de Kirchhoff fica:
 (n parcelas)
(n parcelas)
ou
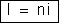
A 2a
lei de Kirchhoff fica:
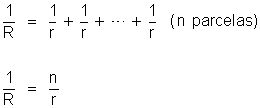
ou
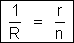
Neste caso
particular a resistência da associação é igual a
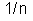 da resistência de cada condutor. E a intensidade da corrente
total é n vezes maior que a corrente de cada condutor.
da resistência de cada condutor. E a intensidade da corrente
total é n vezes maior que a corrente de cada condutor.
