Entre as resistências
de um condutor e suas dimensões existem as duas relações seguintes:
A resistência
elétrica de um condutor homogêneo é diretamente proporcional ao
seu comprimento.
Para demonstrá-la
tomamos diversos condutores, todos de mesmo material, mesma área
de secção transversal e à mesma temperatura, mas de comprimentos
diferentes. Sendo
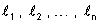os seus comprimentos e
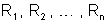as suas resistências, encontramos as seguintes relações:
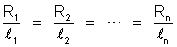
o que demonstra
a lei.
A resistência
elétrica de um condutor homogêneo é inversamente proporcional à
área de sua secção transversal.
Para demonstrá-la
consideramos diversos condutores todos de mesmo material, mesmo
comprimento e à mesma temperatura, mas com áreas de secções transversais
diferentes. Medindo as áreas
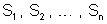dessas secções e
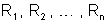as resistências dos condutores, encontramos as seguintes
relações:
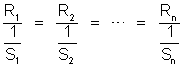
ou
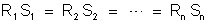
o que demonstra
a lei.
Essas duas leis
podem ser expressas por uma única fórmula. Representando por
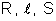respectivamente a resistência, o comprimento e a área da
secção transversal de um condutor, temos:
pela 1a
lei, R é diretamente proporcional a
;
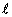pela 2a
lei, R é diretamente proporcional a
;
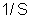logo, R é
diretamente proporcional a
;
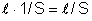isto é,
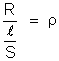(constante)
ou
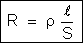
A quantidade
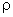varia de um material para outro, e, para um mesmo material,
varia com a temperatura. É chamada resistividade, ou resistência
específica do material.
Para definirmos
resistividade de um material à certa temperatura consideramos um
fio feito com esse material e tendo comprimento
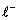, área de secção transversal S e resistência R. Por definição,
chama-se resistividade do material, à temperatura em que se encontra
o fio, ao quociente
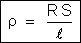
A importância
desse conceito está no fato de que, para uma dada temperatura, o
quociente indicado é constante para um dado material, e não depende
do fio particular usado para calculá-lo.
Se
na expressão anterior considerarmos
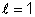e
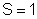, teremos:
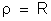numericamente
o
que significa que: a resistividade de um material é numericamente
igual à resistência de um fio feito com esse material e tendo
unidade de comprimento, e unidade de área em secção transversal.
