
Chama-se linha
de força de um campo elétrico a uma linha que em cada
ponto é tangente ao vetor campo desse ponto.
Assim, se nos
pontos A, B, C, D,... o vetor campo é respectivamente
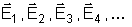 a linha de força que passa por todos esses pontos é
a linha ABCD... tangente a
a linha de força que passa por todos esses pontos é
a linha ABCD... tangente a
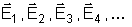 (fig. 46).
(fig. 46).

Figura 46
Não
é só o campo elétrico que tem linhas de força.
O campo magnético e o da gravidade, por exemplo, também
tem. No caso da gravidade, a linha de força é
uma linha que em todos os seus pontos se mantém tangente
ao vetor aceleração da gravidade,
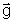 ;
sabemos que a linha que satisfaz a essa condição é
a vertical; isto é, as linhas de força do campo gravitacional
são as verticais.
;
sabemos que a linha que satisfaz a essa condição é
a vertical; isto é, as linhas de força do campo gravitacional
são as verticais.
A linha de força tem, assim, uma definição
puramente geométrica. Mas, vejamos duas conclusões
que podemos tirar dessa definição.
1a
conclusão – Se conhecemos uma linha de força
ABCD..., saberemos qual a direção do campo
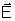 em qualquer um de seus pontos; é a direção
da tangente à linha nesse ponto.
em qualquer um de seus pontos; é a direção
da tangente à linha nesse ponto.
2a
conclusão – Suponhamos uma carga q colocada
em um ponto A de uma linha de força (fig. 47). O campo
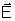 é tangente à linha de força no ponto
A. A força
é tangente à linha de força no ponto
A. A força
 que atua em q, que vale
que atua em q, que vale
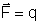 . .
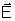 ,
tem a mesma direção que ,
tem a mesma direção que
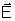 ;
logo ;
logo
 ,
também é tangente à linha de força
no ponto A. Portanto, em cada ponto, a tangente à
linha de força dá a direção
de força que atua numa carga elétrica posta
nesse ponto. ,
também é tangente à linha de força
no ponto A. Portanto, em cada ponto, a tangente à
linha de força dá a direção
de força que atua numa carga elétrica posta
nesse ponto. |
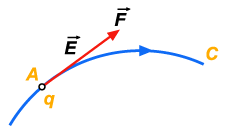 Figura 47 Figura 47 |
Para fixar
idéias, consideremos as linhas de força do campo gravitacional,
isto é, as verticais. As duas conclusões apresentadas
acima para o campo elétrico também valem para o campo
gravitacional, e são bem conhecidas de todos. Assim, a primeira
conclusão significa que, se conhecermos uma vertical, como
consequência conheceremos a direção da aceleração
da gravidade
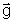 em cada um de seus pontos: é a tangente à vertical.
A segunda conclusão significa que, em cada ponto, a tangente
à vertical dá a direção da força
com que a Terra atrai um corpo. Qual o interesse de conhecermos
as linhas de força de um campo elétrico? A importância
das linhas de força está exatamente nas duas conclusões
citadas acima. É que, conhecendo as linhas de força,
conhecemos as direções do vetor
em cada um de seus pontos: é a tangente à vertical.
A segunda conclusão significa que, em cada ponto, a tangente
à vertical dá a direção da força
com que a Terra atrai um corpo. Qual o interesse de conhecermos
as linhas de força de um campo elétrico? A importância
das linhas de força está exatamente nas duas conclusões
citadas acima. É que, conhecendo as linhas de força,
conhecemos as direções do vetor
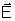 e das forças que atuam nas cargas colocadas no campo. É
por isso que costumamos representar geometricamente um campo elétrico
por meio das suas linhas de força. É o caso da figura
abaixo em que o campo
é formado por duas cargas elétricas, sendo uma positiva
e uma negativa,
e das forças que atuam nas cargas colocadas no campo. É
por isso que costumamos representar geometricamente um campo elétrico
por meio das suas linhas de força. É o caso da figura
abaixo em que o campo
é formado por duas cargas elétricas, sendo uma positiva
e uma negativa,

Figura 52
e o da próxima
figura, em que o campo é formado por duas cargas positivas.

Figura 53
Uma
propriedade importante – Duas linhas de força
de um mesmo campo elétrlco nunca se cruzam. A demonstraçao
dessa propriedade se faz por absurdo. Suponhamos que duas
linhas de força (1) e (2) se cruzassem no ponto A (fig. 48).
Como em cada ponto o vetor campo é tangente à
linha de força, concluiríamos que existiria
um vetor
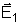 tangente à linha de força (1), e um vetor
tangente à linha de força (1), e um vetor
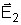 tangente à linha de força (2). Logo, no mesmo
ponto A existiriam dois campos,
tangente à linha de força (2). Logo, no mesmo
ponto A existiriam dois campos,
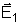 e
e
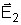 .
Mas, isso não pode acontecer, pois pela propriedade
fundamental do campo elétrico, em cada ponto só
existe um vetor campo, perfeitamente determinado em intensidade,
direção e sentido. .
Mas, isso não pode acontecer, pois pela propriedade
fundamental do campo elétrico, em cada ponto só
existe um vetor campo, perfeitamente determinado em intensidade,
direção e sentido. |
 Figura 48 Figura 48 |
Essa propriedade
mostra então que, apesar de no campo elétrico existir
uma infinidade de linhas de força, por cada ponto do campo
passa uma e uma só linha de força.
Exemplos
de linhas de força

Suponhamos
o campo elétrico produzido por uma única carga elétrica
. Vimos no tópico "Campo
Newtoniano, ou Coulombiano" que o campo
elétrico é coulombiano. Portanto, se colocarmos
uma carga q num ponto A do campo da carga Q, a força
 que atuará em Q e em q terá a direção
da reta r que une as duas cargas (fig. 49). Como o vetor
que atuará em Q e em q terá a direção
da reta r que une as duas cargas (fig. 49). Como o vetor
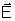 no ponto A tem a mesma direção que a força
no ponto A tem a mesma direção que a força
 ,
então
,
então
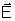 tem a direção da reta r. Isso, qualquer que seja
o ponto A da reta r em que for colocada a carga q. Mas, se em
todos os pontos da reta r os vetores
tem a direção da reta r. Isso, qualquer que seja
o ponto A da reta r em que for colocada a carga q. Mas, se em
todos os pontos da reta r os vetores
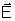 tem a própria direção da reta r, esta reta
é tangente a todos esses vetores: logo, ela é uma
linha de força.
tem a própria direção da reta r, esta reta
é tangente a todos esses vetores: logo, ela é uma
linha de força.
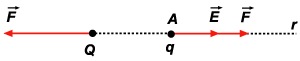
Figura 49
Concluímos
que as linhas de força do campo elétrico produzido
por uma só carga puntiforme são retas que passam
por essa carga. Veja os exemplos das figuras abaixo.
 Figura 50 Figura 50 |
 Figura 51 Figura 51 |

Quando o campo
elétrico é produzido por mais que uma carga as linhas
de força não são mais retas: são curvas.
Como por exemplo:

Figura 52

| Atribuímos
um sentido positivo de percurso a uma linha de força.
Consideramos como positivo o sentido em que seria deslocada
uma carga elétrica puntiforme positiva colocada sobre
a linha. Na figura ao lado a carga puntiforme positiva q seria
deslocada de A para B. Logo, esse é o sentido da linha
de força. |
 Figura 47 Figura 47 |
Vimos
acima que, quando o campo é produzido por uma só
carga puntiforme Q, as linhas de força são
retas que passam por essa carga. Suponhamos que a carga
Q que produz o campo seja positiva; então uma carga
q positiva colocada no ponto A será repelida; logo,
o sentido da linha de força é o sentido QA.
|
 Figura 50 Figura 50 |
Suponhamos
agora que a carga Q que produz o campo seja negativa; então
uma carga q positiva, colocada no ponto A será atraída;
logo, o sentido da linha de força é AQ. Costumamos
exprimir esses fatos dizendo que quando Q é positiva
as linhas de força “saem” da carga; e
que, quando Q é negativa as linhas de força
“entram” na carga.
|
 Figura 51 Figura 51 |
É fácil
verificar que na figura a seguir o sentido das linhas de força
é o que está assinalado.

Figura 53

