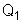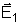Suponhamos duas cargas elétricas pontuais Q₁ e Q₂ suficientemente próximas para que haja uma interpenetração de seus campos. Haverá pontos. como A, sujeitos simultaneamente aos dois campos elétricos. Se existisse só a carga , ela produziria em A, um campo . Se existisse só 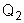, ela produziria em A um campo 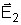. 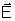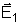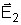A experiência nos mostra que o campo que realmente existe em A é o campo obtido pela soma vetorial dos dois campos e (fig. 45). Esse fato, de que os vetores campos de um mesmo ponto são somados, é um caso particular de um princípio geral que existe em eletricidade e que se chama princípio da superposição dos efeitos. De acordo com esse princípio, quando vários efeitos são produzidos simultaneamente num ponto, esses efeitos se somam. Se os efeitos são representados por grandezas escalares elas são somadas escalarmente; se são representados por grandezas vetoriais elas são somadas vetorialmente.

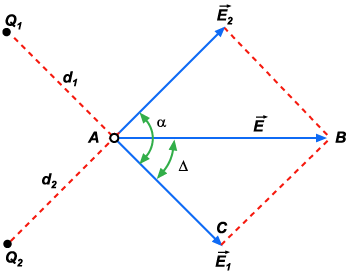
Figura 45

O campo 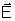resultante tem as seguintes características:

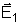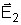Sendo o ângulo formado por e , temos:

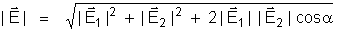
Podemos assinalar a direção do campo 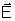em relação a um dos componentes. Chamado ao ângulo que 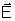faz com 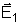, temos:

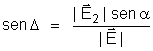
Não podemos exprimir algebricamente.

Quando existirem mais que duas cargas elétricas pontuais produzindo o campo, calculamos o campo devido a cada carga separadamente, e efetuamos a soma vetorial de todos os campos parciais.