| |
Na seção
precedente introduzimos o conceito de comprimento de coerência
transversal entre duas fontes pontuais completamente incoerentes.
Este conceito pode ser utilizado na medida de diâmetros angulares
de estrelas distantes. Se ao invés de duas fontes pontuais
tivermos uma fonte circular, é possível mostrar que
o comprimento de coerência transversal é dado por:
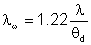
onde o fator 1.22 corresponde ao primeiro zero da função
de Bessel de primeira ordem dividido por
 .
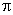Esta expressão também aparece na difração
por uma fenda circular que veremos no próximo capítulo.
Inicialmente selecionamos o comprimento de onda de alguma raia espectral
emitida pela estrela por meio de um filtro óptico de banda
estreita. A seguir, realizamos o experimento de interferência
de Young, numa configuração em que é possível
variar a distância (e portanto o grau de coerência) entre
as duas fendas. Na situação em que a distância
h entre as fendas é
 ,
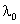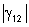se torna nulo e as franjas de interferência desaparecem. Desta
forma podemos encontrar
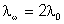e determinar o diâmetro angular
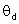da estrela. Como as estrelas se encontram muito distantes da Terra,
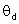é muito pequeno (da ordem de centésimos de segundo de
arco) e assim
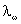é da ordem de metros.
Uma maneira alternativa de se medir diâmetros estrelares com
uma precisão melhor foi proposta por Hanbury-Brown e Twiss.
Este método, conhecido como interferometria de intensidades,
mede a função de coerência de segunda ordem dos
campos, isto é,
 ,
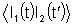onde I1 e I2 são as intensidades nos
detetores 1 e 2, mostrados na Fig. 8.11. É possível
mostrar que a coerência de segunda ordem exibe um efeito de
interferência similar ao mostrado na Fig. 8.9. Ao invés
de se variar a distância entre os detetores, como se faz com
as duas fendas da experiência de Young, é introduzida
uma linha de atraso eletrônica depois de um dos detetores (para
variar o tempo t’) e desta forma os detetores podem ficar estacionários,
separados por uma distância de vários quilômetros,
o que permite a medida de diâmetros angulares muito pequenos,
da ordem de milionésimos de segundo de arco.
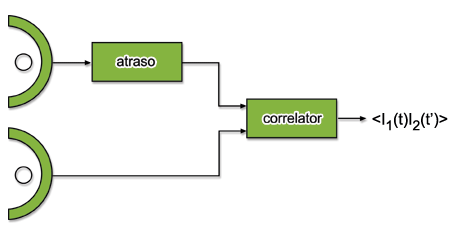
Fig. 8.11 - Interferometria
de intensidade para medir diâmetros de estrelas.
Sergio Carlos Zilio
|
|
