|

Uma
das aplicações da interferência de múltiplos
feixes é na confecção de componentes ópticos
que transmitem ou refletem seletivamente a radiação
eletromagnética. Tais componentes são feitos depositando-se
filmes finos de materiais dielétricos sobre um substrato de
vidro ou quartzo opticamente plano. Os materiais mais utilizados para
este fim são: MgF2 (n = 1,38), SiO2 (1,45),
ZnS(n = 2,38), cridita (n = 1,34), TiO2 (n = 2.2), ZnO2,
CSF etc.
No tratamento deste problema não usaremos a soma de campos
transmitidos ou refletidos como foi feito o interferômetro de
Fabry-Perot. Ao invés, faremos uso das condições
de contorno para 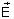 e
e 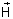 nas interfaces entre os filmes. Considere 3 meios com índices
de refração n0, n1 e n2
conforme mostra a Fig. 7.15. O campo
nas interfaces entre os filmes. Considere 3 meios com índices
de refração n0, n1 e n2
conforme mostra a Fig. 7.15. O campo
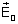 incide do meio n0 sobre o meio n1. O campo
total refletido é incide do meio n0 sobre o meio n1. O campo
total refletido é
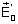 .
No meio n1 o campo total caminhando para a direita é .
No meio n1 o campo total caminhando para a direita é
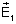 e para a esquerda
e para a esquerda
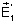 e no meio n2 o campo total transmitido é
e no meio n2 o campo total transmitido é
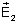 caminhando para a direita. Como as polarizações
não se alteram na passagem de um meio para o outro, podemos
escrever as condições de contorno para os módulos
de caminhando para a direita. Como as polarizações
não se alteram na passagem de um meio para o outro, podemos
escrever as condições de contorno para os módulos
de
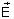 e e
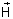 como: como:
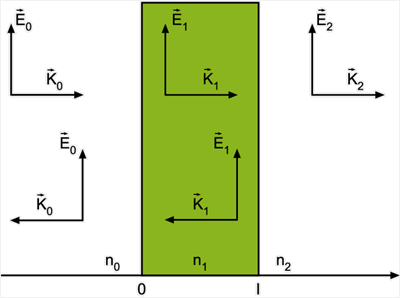
Fig. 7.15 - Geometria dos campos elétricos para a determinação
das condições de contorno.
| Em x = 0: |
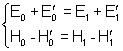 |
(7.41a)
|
| Em x = l: |
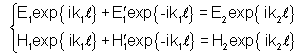 |
(7.41a)
|
Como H=nE/mc, as duas equações
envolvendo o campo magnético se transformam em:
Das
equações anteriores para o campo elétrico e destas
duas últimas sai que:
Lembrando-se
que
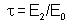 e
e
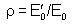 ,
e que o fator ,
e que o fator
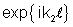 não é importante pois sempre estamos interessados em
não é importante pois sempre estamos interessados em
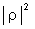 e
e
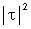 ,
podemos escrever as equações acima na forma matricial: ,
podemos escrever as equações acima na forma matricial:
onde M é chamada de matriz de transferência do filme
n1. Podemos generalizar este raciocínio para N filmes:
onde
M1M2...MN =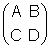 é a matriz de transferência para N filmes. Da igualdade
matricial acima obtém-se:
é a matriz de transferência para N filmes. Da igualdade
matricial acima obtém-se:
A
seguir vamos ver duas aplicações simples do que foi
exposto acima.

Tomemos inicialmente apenas uma película. Através da
eq. (7.44) vemos que a matriz de transferência deste filme possui
os elementos A = cos k1l,
B = i sen k1l/ n1,
C = i n1 sen k1l
e D = cos k1l, que quando
substituidos na eq. (7.46.a) resulta em:
Se k1l =p
/2 temos
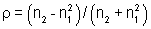 e portanto, R =
e portanto, R =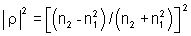 . Se quisermos uma película anti-refletora
. Se quisermos uma película anti-refletora
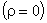 as seguintes condições devem ser satisfeitas: as seguintes condições devem ser satisfeitas:

Considere agora 2N películas onde as ímpares têm
espessura li/4 e índice
de refração n1, enquanto que as pares possuem
espessura lp/4 e índice
de refração np conforme mostra a Fig. 7.16.
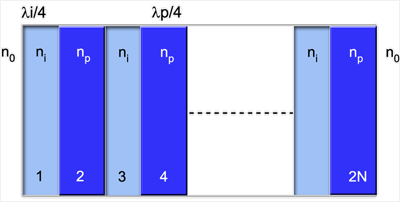
Fig. 7.16 - Configuração para um espelho de alta refletividade.
As matrizes de transferência para as ímpares e pares
são:
Portanto,
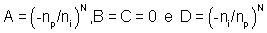 e assim, tomando n0 = 1 temos:
e assim, tomando n0 = 1 temos:
Quando n ~ n0 = 1 e N muito grande,
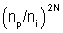 ~
0 pois np < ni e portanto R ~ 1. ~
0 pois np < ni e portanto R ~ 1.
Sergio Carlos Zilio
|