|

Considere um campo
elétrico onde as componentes x e y estão defasadas de
um ângulo d:
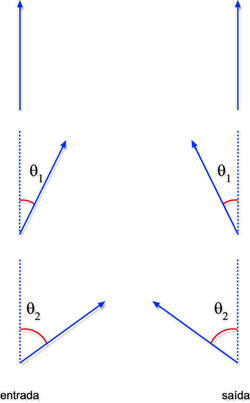
Fig. 6.20 - Rotação do plano de polarização
da luz pela ação do dispositivo da Fig. 6.19(b)
Jones escreveu
este campo da forma matricial:
Usando este formalismo
podemos escrever o campo elétrico para as várias polarizações
já vistas:
e ainda definir
operações tais como:
(ii) Produto escalar:
tomando
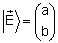 e e
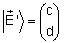 temos:
temos:
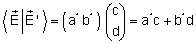 .
Dois vetores são ortogonais quando .
Dois vetores são ortogonais quando
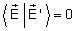 . Exemplo: . Exemplo: 
Dentro deste esquema podemos associar a cada sistema óptico
uma matriz que modifica o campo incidente, dando origem ao campo emergente
desejado, de maneira análoga ao que foi feito na óptica
geométrica. Vamos escrever as matrizes para os elementos já
vistos:

devemos ter
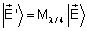 ,
onde ,
onde
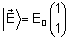 , ,
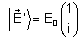 e
e
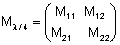 .
Realizando o produto matricial temos: .
Realizando o produto matricial temos:
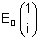 =
=
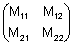
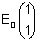 . .
Logo, 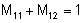 e
e 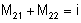 .
Existem várias matrizes que satisfazem estas condições.
Devemos lembrar que se o campo tem polarização ao longo
de um dos eixos principais, esta polarização não
é alterada. Assim, temos: .
Existem várias matrizes que satisfazem estas condições.
Devemos lembrar que se o campo tem polarização ao longo
de um dos eixos principais, esta polarização não
é alterada. Assim, temos:
e desta forma
a matriz que descreve a lâmina de quarto de onda é:

procedendo de
maneira análoga podemos encontrar a matriz para a lâmina
l/2:

considere um campo
elétrico linearmente polarizado, formando um ângulo q
com o eixo x e propagando-se na direção z. A Fig. 6.21
mostra este campo incidindo num polarizador com eixo de transmissão
na direção x. Neste caso temos:
A intensidade
de luz emergente é proporcional a:
Esta é
a lei de Malus, que não vale para um polaróide porque
ele não extingue completamente a componente y, mas vale para
o prisma de Nicol.
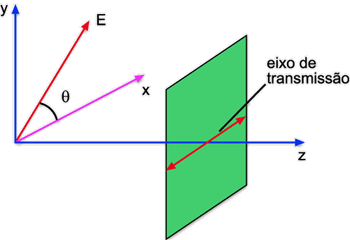
Fig. 6.21 - Polarizador com eixo de transmissão horizontal.

o campo incidente
é o mesmo que o do caso anterior, mas o eixo de transmissão
do polarizador faz 450 com o eixo
x, conforme mostra a Fig. 6.22.
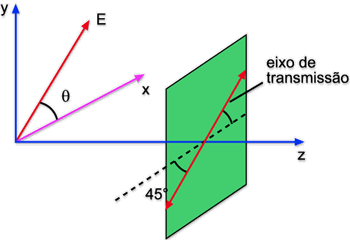
Fig. 6.22 - Polarizador com eixo de transmissão a 450.
Na
direção do eixo de transmissão, o campo incidente
é
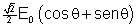 que
é também o campo emergente. Decompondo-o em duas componentes,
Ex' e Ey', obtém-se: que
é também o campo emergente. Decompondo-o em duas componentes,
Ex' e Ey', obtém-se:
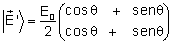
para
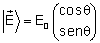 ,
de onde se tira a matriz para este sistema: ,
de onde se tira a matriz para este sistema:
Sergio Carlos Zilio
|